CHAPTER I GENERAL PRINCIPLES OF NUCLEAR EXPLOSIONS
CHARACTERISTICS OF NUCLEAR EXPLOSIONS
INTRODUCTION
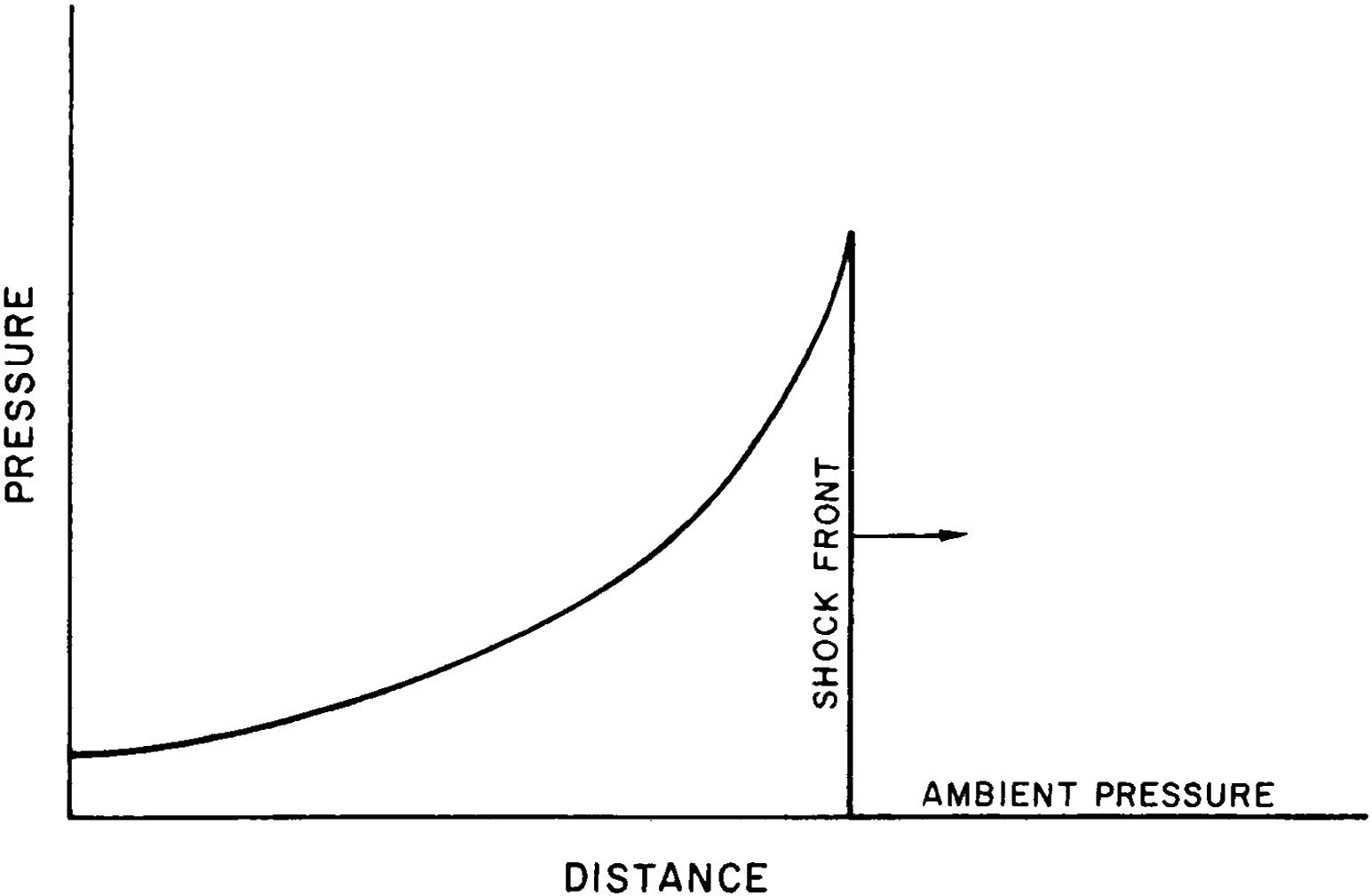
1.01 An explosion, in general, results from the very rapid release of a large amount of energy within a limited space. This is true for a conventional “high explosive,” such as TNT, as well as for a nuclear (or atomic) explosion,1 although the energy is produced in quite different ways (§ 1.11). The sudden liberation of energy causes a considerable increase of temperature and pressure, so that all the materials present are converted into hot, compressed gases. Since these gases are at very high temperatures and pressures, they expand rapidly and thus initiate a pressure wave, called a “shock wave,” in the surrounding medium-air, water, or earth. The characteristic of a shock wave is that there is (ideally) a sudden increase of pressure at the front, with a gradual decrease behind it, as shown in Fig. 1.01. A shock wave in air is generally referred to as a “blast wave” because it resembles and is accompanied by a very strong wind. In water or in the ground, however, the term “shock” is used, because the effect is like that of a sudden impact.
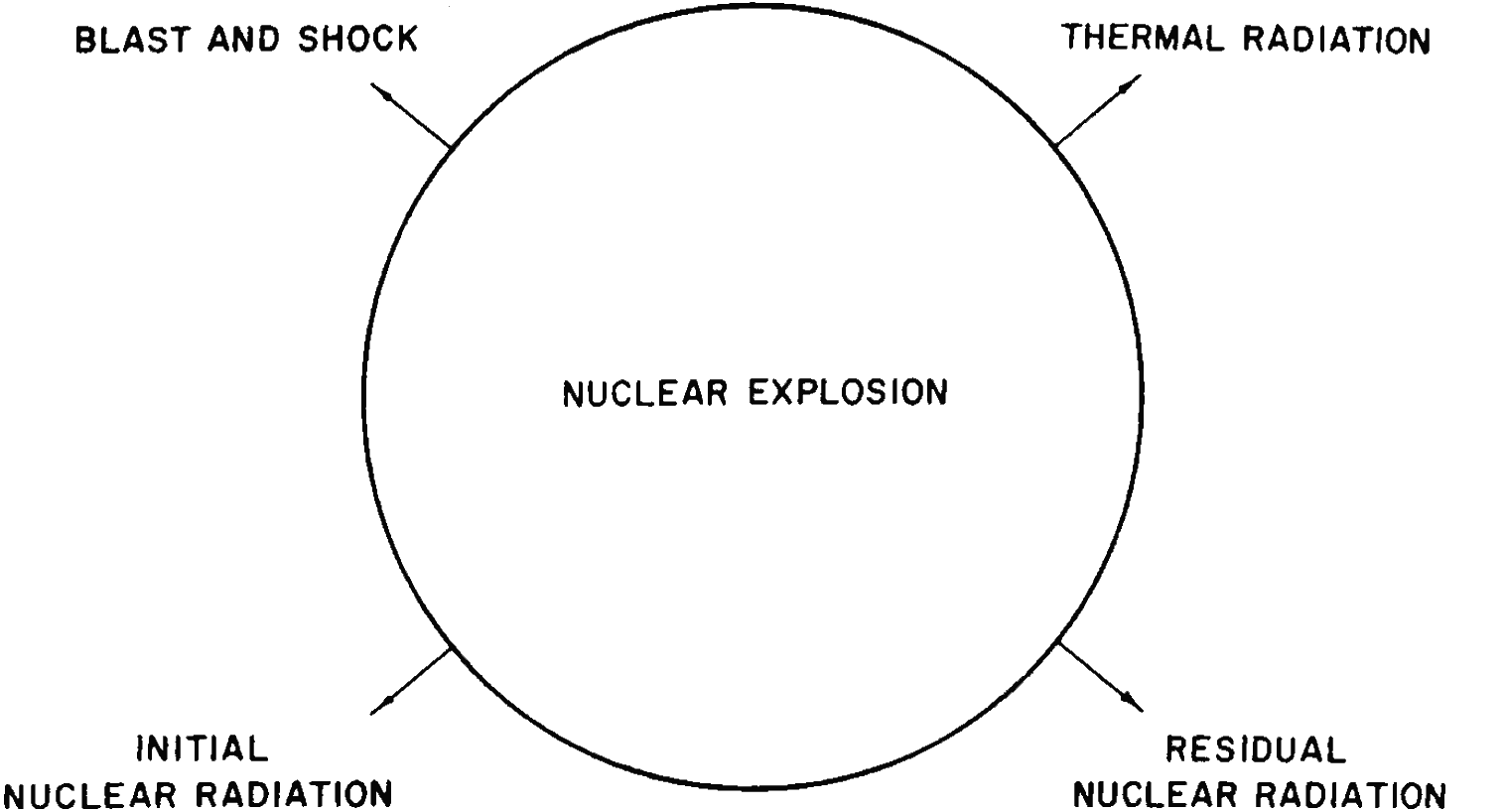
1.02 Nuclear weapons are similar to those of more conventional types insofar as their destructive action is due mainly to blast or shock. On the other hand, there are several basic differences between nuclear and high-explosive weapons. In the first place, nuclear explosions can be many thousands (or millions) of times more powerful than the largest conventional detonations. Second, for the release of a given amount of energy, the mass of a nuclear explosive would be much less than that of a conventional high explosive. Consequently, in the former case, there is a much smaller amount of material available in the weapon itself that is converted into the hot, compressed gases mentioned above. This results in somewhat different mechanisms for the initiation of the blast wave. Third, the temperatures reached in a nuclear explosion are very much higher than in a conventional explosion, and a fairly large proportion of the energy in a nuclear explosion is emitted in the form of light and heat, generally referred to as “thermal radiation.” This is capable of causing skin burns and of starting fires at considerable distances. Fourth, the nuclear explosion is accompanied by highly-penetrating and harmful invisible rays, called the “initial nuclear radiation.” Finally the substances remaining after a nuclear explosion are radioactive, emitting similar radiations over an extended period of time. This is known as the “residual nuclear radiation” or “residual radioactivity” (Fig. 1.02).
1.03 It is because of these fundamental differences between a nuclear and a conventional explosion, including the tremendously greater power of the former, that the effects of nuclear weapons require special consideration. In this connection, a knowledge and understanding of the mechanical and the various radiation phenomena associated with a nuclear explosion are of vital importance.
1.04 The purpose of this book is to describe the different forms in which the energy of a nuclear explosion are released, to explain how they are propagated, and to show how they may affect people (and other living organisms) and materials. Where numerical values are given for specific observed effects, it should be kept in mind that there are inevitable uncertainties associated with the data, for at least two reasons. In the first place, there are inherent difficulties in making exact measurements of weapons effects. The results are often dependent on circumstances which are difficult, if not impossible, to control, even in a test and certainly cannot be predicted in the event of an attack. Furthermore, two weapons producing the same amount of explosive energy may have different quantitative effects because of differences in composition and design.
1.05 It is hoped, nevertheless, that the information contained in this volume, which is the best available, may be of assistance to those responsible for defense planning and in making preparations to deal with the emergencies that may arise from nuclear warfare. In addition, architects and engineers may be able to utilize the data in the design of structures having increased resistance to damage by blast, shock, and fire, and which provide shielding against nuclear radiations.
ATOMIC STRUCTURE AND ISOTOPES
1.06 All substances are made up from one or more of about 90 different kinds of simple materials known as “elements.” Among the common elements are the gases hydrogen, oxygen, and nitrogen; the solid nonmetals carbon, sulfur, and phosphorus; and various metals, such as iron, copper, and zinc. A less familiar element, which has attained prominence in recent years because of its use as a source of nuclear energy, is uranium, normally a solid metal.
1.07 The smallest part of any element that can exist, while still retaining the characteristics of the element, is called an “atom” of that element. Thus, there are atoms of hydrogen, of iron, of uranium, and so on, for all the elements. The hydrogen atom is the lightest of all atoms, whereas the atoms of uranium are the heaviest of those found on earth. Heavier atoms, such as those of plutonium, also important for the release of nuclear energy, have been made artificially (§ 1.14). Frequently, two or more atoms of the same or of different elements join together to form a “molecule.”
1.08 Every atom consists of a relatively heavy central region or “nucleus,” surrounded by a number of very light particles known as “electrons.” Further, the atomic nucleus is itself made up of a definite number of fundamental particles, referred to as “protons” and “neutrons.” These two particles have almost the same mass, but they differ in the respect that the proton carries a unit charge of positive electricity whereas the neutron, as its name implies, is uncharged electrically, i.e., it is neutral. Because of the protons present in the nucleus, the latter has a positive electrical charge, but in the normal atom this is exactly balanced by the negative charge carried by the electrons surrounding the nucleus.
1.09 The essential difference between atoms of different elements lies in the number of protons (or positive charges) in the nucleus; this is called the “atomic number” of the element. Hydrogen atoms, for example, contain only one proton, helium atoms have two protons, uranium atoms have 92 protons, and plutonium atoms 94 protons. Although all the nuclei of a given element contain the same number of protons, they may have different numbers of neutrons. The resulting atomic species, which have identical atomic numbers but which differ in their masses, are called “isotopes” of the particular element. All but about 20 of the elements occur in nature in two or more isotopic forms, and many other isotopes, which are unstable, i.e., radioactive, have been obtained in various ways.
1.10 Each isotope of a given element is identified by its “mass number,” which is the sum of the numbers of protons and neutrons in the nucleus. For example, the element uranium, as found in nature, consists mainly of two isotopes with mass numbers of 235 and 238; they are consequently referred to as uranium-235 and uranium-238, respectively. The nuclei of both isotopes contain 92 protons-as do the nuclei of all uranium isotopes-but the former have in addition 143 neutrons and the latter 146 neutrons. The general term “nuclide” is used to describe any atomic species distinguished by the composition of its nucleus, i.e., by the number of protons and the number of neutrons. Isotopes of a given element are nuclides having the same number of protons but different numbers of neutrons in their nuclei.
1.11 In a conventional explosion, the energy released arises from chemical reactions; these involve a rearrangement among the atoms, e.g., of hydrogen, carbon, oxygen, and nitrogen, present in the chemical high-explosive material. In a nuclear explosion, on the other hand, the energy is produced as a result of the formation of different atomic nuclei by the redistribution of the protons and neutrons within the interacting nuclei. What is sometimes referred to as atomic energy is thus actually nuclear energy, since it results from particular nuclear interactions. It is for the same reason, too, that atomic weapons are preferably called “nuclear weapons.” The forces between the protons and neutrons within atomic nuclei are tremendously greater than those between the atoms; consequently, nuclear energy is of a much higher order of magnitude than conventional (or chemical) energy when equal masses are considered.
1.12 Many nuclear processes are known, but not all are accompanied by the release of energy. There is a definite equivalence between mass and energy, and when a decrease of mass occurs in a nuclear reaction there is an accompanying release of a certain amount of energy related to the decrease in mass. These mass changes are really a reflection of the difference in the internal forces in the various nuclei. It is a basic law of nature that the conversion of any system in which the constituents are held together by weaker forces into one in which the forces are stronger must be accompanied by the release of energy, and a corresponding decrease in mass.
1.13 In addition to the necessity for the nuclear process to be one in which there is a net decrease in mass, the release of nuclear energy in amounts sufficient to cause an explosion requires that the reaction should be able to reproduce itself once it has been started. Two kinds of nuclear interactions can satisfy the conditions for the production of large amounts of energy in a short time. They are known as “fission” (splitting) and “fusion” (joining together). The former process takes place with some of the heaviest (high atomic number) nuclei; whereas the latter, at the other extreme, involves some of the lightest (low atomic number) nuclei.
1.14 The materials used to produce nuclear explosions by fission are certain isotopes of the elements uranium and plutonium. As noted above, uranium in nature consists mainly of two isotopes, namely, uranium-235 (about 0. 7 percent), and uranium-238 (about 99.3 percent). The less abundant of these isotopes, i.e., uranium-235, is the readily fissionable species that is commonly used in nuclear weapons. Another isotope, uranium-233, does not occur naturally, but it is also readily fissionable and it can be made artificially starting with thorium-232. Since only insignificant amounts of the element plutonium are found in nature, the fissionable isotope used in nuclear weapons, plutonium-239, is made artificially from uranium-238.
1.15 When a free (or unattached) neutron enters the nucleus of a fissionable atom, it can cause the nucleus to split into two smaller parts. This is the fission process, which is accompanied by the release of a large amount of energy. The smaller (or lighter) nuclei which result are called the “fission products.” The complete fission of I pound of uranium or plutonium releases as much explosive energy as does the explosion of about 8,000 (short) tons of TNT.
1.16 In nuclear fusion, a pair of light nuclei unite (or fuse) together to form a nucleus of a heavier atom. An example is the fusion of the hydrogen isotope known as deuterium or “heavy hydrogen.” Under suitable conditions, two deuterium nuclei may combine to form the nucleus of a heavier element, helium, with the release of energy. Other fusion reactions are described in § 1.69.
1.17 Nuclear fusion reactions can be brought about by means of very high temperatures, and they are thus referred to as “thermonuclear processes.” The actual quantity of energy liberated, for a given mass of material, depends on the particular isotope (or isotopes) involved in the nuclear fusion reaction. As an example, the fusion of all the nuclei present in 1 pound of the hydrogen isotope deuterium would release roughly the same amount of energy as the explosion of 26,000 tons of TNT.
1.18 In certain fusion processes, between nuclei of the hydrogen isotopes, neutrons of high energy are liberated (see § 1.72). These can cause fission in the most abundant isotope (uranium-238) in ordinary uranium as well as in uranium-235 and plutonium- 239. Consequently, association of the appropriate fusion reactions with natural uranium can result in an extensive utilization of the latter for the release of energy. A device in which fission and fusion (thermonuclear) reactions are combined can therefore produce an explosion of great power. Such weapons might typically release about equal amounts of explosive energy from fission and from fusion.
1.19 A distinction has sometimes been made between atomic weapons, in which the energy arises from fission, on the one hand, and hydrogen (or thermonuclear) weapons, involving fusion, on the other hand. In each case, however, the explosive energy results from nuclear reactions, so that they are both correctly described as nuclear weapons. In this book, therefore, the general terms “nuclear bomb” and “nuclear weapon” will be used, irrespective of the type of nuclear reaction producing the energy of the explosion.
ENERGY YIELD OF A NUCLEAR EXPLOSION
1.20 The “yield” of a nuclear weapon is a measure of the amount of explosive energy it can produce. It is the usual practice to state the yield in terms of the quantity of TNT that would generate the same amount of energy when it explodes. Thus, a 1-kiloton nuclear weapon is one which produces the same amount of energy in an explosion as does 1 kiloton (or 1,000 tons) of TNT. Similarly, a 1-megaton weapon would have the energy equivalent of 1 million tons (or 1,000 kilotons) of TNT. The earliest nuclear bombs, such as were dropped over Japan in 1945 and used in the tests at Bikini in 1946, released very roughly the same quantity of energy as 20,000 tons (or 20 kilotons) of TNT (see, however, § 2.24). Since that time, much more powerful weapons, with energy yields in the megaton range, have been developed.
1.21 From the statement in § 1.15 that the fission of 1 pound of uranium or plutonium will release the same amount of explosive energy as about 8,000 tons of TNT, it is evident that in a 20-kiloton nuclear weapon 2.5 pounds of material undergo fission. However, the actual weight of uranium or plutonium in such a weapon is greater than this amount. In other words, in a fission weapon, only part of the nuclear material suffers fission. The efficiency is thus said to be less than 100 percent. The material that has not undergone fission remains in the weapon residues after the explosion.
DISTRIBUTION OF ENERGY IN NUCLEAR EXPLOSIONS
1.22 It has been mentioned that one important difference between nuclear and conventional (or chemical) explosions is the appearance of an appreciable proportion of the energy as thermal radiation in the former case. The basic reason for this difference is that, weight for weight, the energy produced by a nuclear explosive is millions of times as great as that produced by a chemical explosive. Consequently, the temperatures reached in the former case are very much higher than in the latter, namely, tens of millions of degrees in a nuclear explosion compared with a few thousands in a conventional explosion. As a result of this great difference in temperature, the distribution of the explosion energy is quite different in the two cases.
1.23 Broadly speaking, the energy may be divided into three categories: kinetic (or external) energy, i.e., energy of motion of electrons, atoms, and molecules as a whole; internal energy of these particles; and thermal radiation energy. The proportion of thermal radiation energy increases rapidly with increasing temperature. At the moderate temperatures attained in a chemical explosion, the amount of thermal radiation is comparatively small, and so essentially all the energy released at the time of the explosion appears as kinetic and internal energy. This is almost entirely converted into blast and shock, in the manner described in § 1.01. Because of the very much higher temperatures in a nuclear explosion, however, a considerable proportion of the energy is released as thermal radiation. The manner in which this takes place is described later (§ 1.77 et seq.).
1.24 The fraction of the explosion energy received at a distance from the burst point in each of the forms depicted in Fig. 1.02 depends on the nature and yield of the weapon and particularly on the environment of the explosion. For a nuclear detonation in the atmosphere below an altitude of about 100,000 feet, from 35 to 45 percent of the explosion energy is received as thermal energy in the visible and infrared portions of the spectrum (see Fig. 1.74). In addition, below an altitude of about 40,000 feet, about 50 percent of the explosive energy is used in the production of air shock. At somewhat higher altitudes, where there is less air with which the energy of the exploding nuclear weapon can interact, the proportion of energy converted into shock is decreased whereas that emitted as thermal radiation is correspondingly increased (§ 1.36).
1.25 The exact distribution of energy between air shock and thermal radiation is related in a complex manner to the explosive energy yield, the burst altitude, and, to some extent, to the weapon design, as will be seen in this and later chapters. However, an approximate rule of thumb for a fission weapon exploded in the air at an altitude of less than about 40,000 feet is that 35 percent of the explosion energy is in the form of thermal radiation and 50 percent produces air shock. Thus, for a burst at moderately low altitudes, the air shock energy from a fission weapon will be about half of that from a conventional high explosive with the same total energy release; in the latter, essentially all of the explosive energy is in the form of air blast. This means that if a 20-kiloton fission weapon, for example, is exploded in the air below 40,000 feet or so, the energy used in the production of blast would be roughly equivalent to that from 10 kilotons of TNT.
1.26 Regardless of the height of burst, approximately 85 percent of the explosive energy of a nuclear fission weapon produces air blast (and shock), thermal radiation, and heat. The remaining 15 percent of the energy is released as various nuclear radiations. Of this, 5 percent constitutes the initial nuclear radiation, defined as that produced within a minute or so of the explosion (§ 2.42). The final 10 percent of the total fission energy represents that of the residual (or delayed) nuclear radiation which is emitted over a period of time. This is largely due to the radioactivity of the fission products present in the weapon residues (or debris) after the explosion. In a thermonuclear device, in which only about half of the total energy arises from fission (§ 1.18), the residual nuclear radiation carries only 5 percent of the energy released in the explosion. It should be noted that there are no nuclear radiations from a conventional explosion since the nuclei are unaffected in the chemical reactions which take place.
1.27 Because about 10 percent of the total fission energy is released in the form of residual nuclear radiation some time after the detonation, this is not included when the energy yield of a nuclear explosion is stated, e.g., in terms of the TNT equivalent as in § 1.20. Hence, in a pure fission weapon the explosion energy is about 90 percent of the total fission energy, and in a thermonuclear device it is, on the average, about 95 percent of the total energy of the fission and fusion reactions. This common convention will be adhered to in subsequent chapters. For example, when the yield of a nuclear weapon is quoted or used in equations, figures, etc. , it will represent that portion of the energy delivered within a minute or so, and will exclude the contribution of the residual nuclear radiation.
1.28 The initial nuclear radiation consists mainly of “gamma rays,” which are electromagnetic radiations of high energy (see § 1.73) originating in atomic nuclei, and neutrons. These radiations, especially gamma rays, can travel great distances through air and can penetrate considerable thicknesses of material. Although they can neither be seen nor felt by human beings, except at very high intensities which cause a tingling sensation, gamma rays and neutrons can produce harmful effects even at a distance from their source. Consequently, the initial nuclear radiation is an important aspect of nuclear explosions.
1.29 The delayed nuclear radiation arises mainly from the fission products which, in the course of their radioactive decay, emit gamma rays and another type of nuclear radiation called “beta particles.” The latter are electrons, i.e., particles carrying a negative electric charge, moving with high speed; they are formed by a change (neutron -+ proton + electron) within the nuclei of the radioactive atoms. Beta particles, which are also invisible, are much less penetrating than gamma rays, but like the latter they represent a potential hazard.
1.30 The spontaneous emission of beta particles and gamma rays from radioactive substances, i.e., a radioactive nuclide (or radionuclide), such as the fission products, is a gradual process. It takes place over a period of time, at a rate depending upon the nature of the material and upon the amount present. Because of the continuous decay, the quantity of the radionuclide and the rate of emission of radiation decrease steadily. This means that the residual nuclear radiation, due mainly to the fission products, is most intense soon after the explosion but diminishes in the course of time.
TYPES OF NUCLEAR EXPLOSIONS
1.31 The immediate phenomena associated with a nuclear explosion, as well as the effects of shock and blast and of thermal and nuclear radiations, vary with the location of the point of burst in relation to the surface of the earth. For descriptive purposes five types of burst are distinguished, although many variations and intermediate situations can arise in practice. The main types, which will be defined below, are (1) air burst, (2) high-altitude burst, (3) underwater burst, (4) underground burst, and (5) surface burst.
1.32 Provided the nuclear explosion takes place at an altitude where there is still an appreciable atmosphere, e.g., below about 100,000 feet, the weapon residues almost immediately incorporate material from the surrounding medium and form an intensely hot and luminous mass, roughly spherical in shape, called the “fireball.” An “air burst” is defined as one in which the weapon is exploded in the air at an altitude below 100,000 feet, but at such a height that the fireball (at roughly maximum brilliance in its later stages) does not touch the surface of the earth. For example, in the explosion of a 1-megaton weapon the fireball may grow until it is nearly 5,700 feet (1.1 mile) across at maximum brilliance. This means that, in this particular case, the explosion must occur at least 2,850 feet above the earth’s surface if it is to be called an air burst.
1.33 The quantitative aspects of an air burst will be dependent upon its energy yield, but the general phenomena are much the same in all cases. Nearly all of the shock energy that leaves the fireball appears as air blast, although some is generally also transmitted into the ground. The thermal radiation will travel long distances through the air and may be of sufficient intensity to cause moderately severe burns of exposed skin as far away as 12 miles from a 1-megaton explosion, on a fairly clear day. For air bursts of higher energy yields, the corresponding distances will, of course, be greater. The thermal radiation is largely stopped by ordinary opaque materials; hence, buildings and clothing can provide protection.
1.34 The initial nuclear radiation from an air burst will also penetrate a long way in air, although the intensity falls off fairly rapidly at increasing distances from the explosion. The interactions with matter that result in the absorption of energy from gamma rays and from neutrons are quite different, as will be seen in Chapter VIII. Different materials are thus required for the most efficient removal of these radiations; but concrete, especially if it incorporates a heavy element, such as iron or barium, represents a reasonable practical compromise for reducing the intensities of both gamma rays and neutrons. A thickness of about 4 feet of ordinary concrete would probably provide adequate protection from the effects of the initial nuclear radiation for people at a distance of about 1 mile from an air burst of a 1-megaton nuclear weapon. However, at this distance the blast effect would be so great that only specially designed blast-resistant structures would survive.
1.35 In the event of a moderately high (or high) air burst, the fission products remaining after the nuclear explosion will be dispersed in the atmosphere. The residual nuclear radiation arising from these products will be of minor immediate consequence on the ground. On the other hand, if the burst occurs nearer the earth’s surface, the fission products may fuse with particles of earth, part of which will soon fall to the ground at points close to the explosion. This dirt and other debris will be contaminated with radioactive material and will, consequently, represent a possible danger to living things.
1.36 A “high-altitude burst” is defined as one in which the explosion takes place at an altitude in excess of 100,000 feet. Above this level, the air density is so low that the interaction of the weapon energy with the surroundings is markedly different from that at lower altitudes and, moreover, varies with the altitude. The absence of relatively dense air causes the fireball characteristics in a high-altitude explosion to differ from those of an air burst. For example, the fraction of the energy converted into blast and shock is less and decreases with increasing altitude. Two factors affect the thermal energy radiated at high altitude. First, since a shock wave does not form so readily in the less dense air, the fireball is able to radiate thermal energy that would, at lower altitudes, have been used in the production of air blast. Second, the less dense air allows energy from the exploding weapon to travel much farther than at lower altitudes. Some of this energy simply warms the air at a distance from the fireball and it does not contribute to the energy that can be radiated within a short time (§ 1.79). In general, the first of these factors is effective between 100,000 and 140,000 feet, and a larger proportion of the explosion energy is released in the form of thermal radiation than at lower altitudes. For explosions above about 140;000 feet, the second factor becomes the more important, and the fraction of the energy that appears as thermal radiation at the time of the explosion becomes smaller.
1.37 The fraction of the explosion energy emitted from a weapon as nuclear radiations is independent of the height of burst. However, the partition of that energy between gamma rays and neutrons received at a distance will vary since a significant fraction of the gamma rays result from interactions of neutrons with nitrogen atoms in the air at low altitudes. Furthermore, the attenuation of the initial nuclear radiation with increasing distance from the explosion is determined by the total amount of air through which the radiation travels. This means that, for a given explosion energy yield, more initial nuclear radiation will be received at the same slant range on the earth’s surface from a high-altitude detonation than from a moderately high air burst. In both cases the residual radiation from the fission products and other weapon residues will not be significant on the ground (§ 1.35).
1.38 Both the initial and the residual nuclear radiations from high-altitude bursts will interact with the constituents of the atmosphere to expel electrons from the atoms and molecules. Since the electron carries a negative electrical charge, the residual part of the atom (or molecule) is positively charged, i.e., it is a positive ion. This process is referred to as “ionization,” and the separated electrons and positive ions are called “ion pairs.” The existence of large numbers of electrons and ions at high altitudes may have seriously degrading effects on the propagation of radio and radar signals (see Chapter X). The free electrons resulting from gamma-ray ionization of the air in a high-altitude explosion may also interact with the earth’s magnetic field to generate strong electromagnetic fields capable of causing damage to unprotected electrical or electronic equipment located in an extensive area below the burst. The phenomenon known as the “electromagnetic pulse” (or EMP) is described in Chapter XI. The EMP can also be produced in surface and low air bursts, but a much smaller area around the detonation point is affected.
1.39 If a nuclear explosion occurs under such conditions that its center is beneath the ground or under the surface of water, the situation is described as an “underground burst” or an “underwater burst,” respectively. Since some of the effects of these two types of explosions are similar, they will be considered here together as subsurface bursts. In a subsurface burst, most of the shock energy of the explosion appears as underground or underwater shock, but a certain proportion, which is less the greater the depth of the burst, escapes and produces air blast. Much of the thermal radiation and of the initial nuclear radiation will be absorbed within a short distance of the explosion. The energy of the absorbed radiations will merely contribute to the heating of the ground or body of water. Depending upon the depth of the explosion, some of the thermal and nuclear radiations will escape, but the intensities will generally be less than for an air burst. However, the residual nuclear radiation, i.e., the radiation emitted after the first minute, now becomes of considerable significance, since large quantities of earth or water in the vicinity of the explosion will be contaminated with radioactive fission products.
1.40 A “surface burst” is regarded as one which occurs either at or slightly above the actual surface of the land or water. Provided the distance above the surface is not great, the phenomena are essentially the same as for a burst occurring on the surface. As the height of burst increases up to a point where the fireball (at maximum brilliance in its later stages) no longer touches the land or water, there is a transition zone in which the behavior is intermediate between that of a true surface burst and of an air burst. In surface bursts, the air blast and ground (or water) shock are produced in varying proportions depending on the energy of the explosion and the height of burst.
1.41 Although the five types of burst have been considered as being fairly distinct, there is actually no clear line of demarcation between them. It will be apparent that, as the height of the explosion is decreased, a high-altitude burst will become an air burst, and an air burst will become a surface burst. Similarly, a surface burst merges into a subsurface explosion at a shallow depth, when part of the fireball actually breaks through the surface of the land or water. It is nevertheless a matter of convenience, as will be seen in later chapters, to divide nuclear explosions into the five general types defined above.
SCIENTIFIC BASIS OF NUCLEAR EXPLOSIONS2
FISSION ENERGY
1.42 The significant point about the fission of a uranium (or plutonium) nucleus by means of a neutron, in addition to the release of a large quantity of energy, is that the process is accompanied by the instantaneous emission of two or more neutrons; thus, \[ \begin{align} \text{Neutron + } &\!\left\{ \enspace \begin{array}{lr} \text{uranium-235}\\ \text{(or uranium-233)}\\ \text{(or plutonium-239)} \enspace \end{array} \right\} \\ \\ \to&\enspace \begin{array}{lr} \text{fission fragments +}\\ \text{2 or 3 neutrons + energy.} \end{array} \end{align} \] The neutrons liberated in this manner are able to induce fission of additional uranium (or plutonium) nuclei, each such process resulting in the emission of more neutrons which can produce further fission, and so on. Thus, in principle, a single neutron could start off a chain of nuclear fissions, the number of nuclei suffering fission, and the energy liberated, increasing at a tremendous rate, as will be seen shortly.
1.43 There are many different ways in which the nuclei of a given fissionable species can split up into two fission fragments (initial fission products), but the total amount of energy liberated per fission does not vary greatly. A satisfactory average value of this energy is 200 million electron volts. The million electron volt (or 1 MeV) unit has been found convenient for expressing the energy released in nuclear reactions; it is equivalent to 1.6×10-6 erg or 1.6×10-13 joule. The manner in which this energy is distributed among the fission fragments and the various radiations associated with fission is shown in Table 1.43.
| MeV | |
|---|---|
| Kinetic energy of fission fragments | 165 ± 5 |
| Instantaneous gamma ray energy | 7 ± 1 |
| Kinetic energy of fission neutron | 5 ± 0.5 |
| Beta particles from fission products | 7 ± 1 |
| Gamma rays from fission products | 6 ± 1 |
| Neutrinos from fission products | 10 |
| Total energy per fission | 200 ± 6 |
1.44 The results in the table may be taken as being approximately applicable to either uranium-233, uranium-235, or plutonium-239. These are the only three known substances, which are reasonably stable so that they can be stored without appreciable decay, that are capable of undergoing fission by neutrons of all energies. Hence, they are the only materials that can by used to sustain a fission chain. Uranium-238, the most abundant isotope in natural uranium (§ 1.14), and thorium-232 will suffer fission by neutrons of high energy only, but not by those of lower energy. For this reason these substances cannot sustain a chain reaction. However, when fission does occur in these elements, the energy distribution is quite similar to that shown in the table.
1.45 Only part of the fission energy is immediately available in a nuclear explosion; this includes the kinetic energy of the fission fragments, most of the energy of the instantaneous gamma rays, which is converted into other forms of energy within the exploding weapon, and also most of the neutron kinetic energy, but only a small fraction of the decay energy of the fission products. There is some compensation from energy released in reactions in which neutrons are captured by the weapon debris, and so it is usually accepted that about 180 MeV of energy are immediately available per fission. There are 6.02×1023 nuclei in 235 grams of uranium-235 (or 239 grams of plutonium-239), and by making use of familiar conversion factors (cf. § 1.43) the results quoted in Table 1.45 may be obtained for the energy (and other) equivalents of 1 kiloton of TNT. The calculations are based on an accepted, although somewhat arbitrary, figure of 1012 calories as the energy released in the explosion of this amount of TNT.3
EQUIVALENTS OF 1 KILOTON OF TNT
- Complete fission of 0.057kg (57 grams or 2 ounces) fissionable material
- Fission of 1.45 × 1023 nuclei
- 1012 calories
- 2.6 × 1025 million electron volts
- 4.18 × 1019 ergs (4.18 × 1012 joules)
- 1.16 × 106 kilowatt-hours
- 3.97 × 109 British thermal units
CRITICAL MASS FOR A FISSION CHAIN
1.46 Although two to three neutrons are produced in the fission reaction for every nucleus that undergoes fission, not all of these neutrons are available for causing further fissions. Some of the fission neutrons are lost by escape, whereas others are lost in various non-fission reactions. In order to sustain a fission chain reaction, with continuous release of energy, at least one fission neutron must be available to cause further fission for each neutron previously absorbed in fission. If the conditions are such that the neutrons are lost at a faster rate than they are formed by fission, the chain reaction would not be self-sustaining. Some energy would be produced, but the amount would not be large enough, and the rate of liberation would not be sufficiently fast, to cause an effective explosion. It is necessary, therefore, in order to achieve a nuclear explosion, to establish conditions under which the loss of neutrons is minimized. In this connection, it is especially important to consider the neutrons which escape from the substance undergoing fission.
1.47 The escape of neutrons occurs at the exterior of the uranium (or plutonium) material. The rate of loss by escape will thus be determined by the surface area. On the other hand, the fission process, which results in the formation of more neutrons, takes place throughout the whole of the material and its rate is, therefore, dependent upon the mass. By increasing the mass of the fissionable material, at constant density, the ratio of the surface area to the mass is decreased; consequently, the loss of neutrons by escape relative to their formation by fission is decreased. The same result can also be achieved by having a constant mass but compressing it to a smaller volume (higher density), so that the surface area is decreased.
1.48 The situation may be understood by reference to Fig. 1.48 showing two spherical masses, one larger than the other, of fissionable material of the same density. Fission is initiated by a neutron represented by a dot within a small circle. It is supposed that in each act of fission three neutrons are emitted; in other words, one neutron is captured and three are expelled. The removal of a neutron from the system is indicated by the head of an arrow. Thus, an arrowhead within the sphere means that fission has occurred and extra neutrons are produced, whereas an arrowhead outside the sphere implies the loss of a neutron. It is evident from Fig. 1.48 that a much greater fraction of the neutrons is lost from the smaller than from the larger mass.
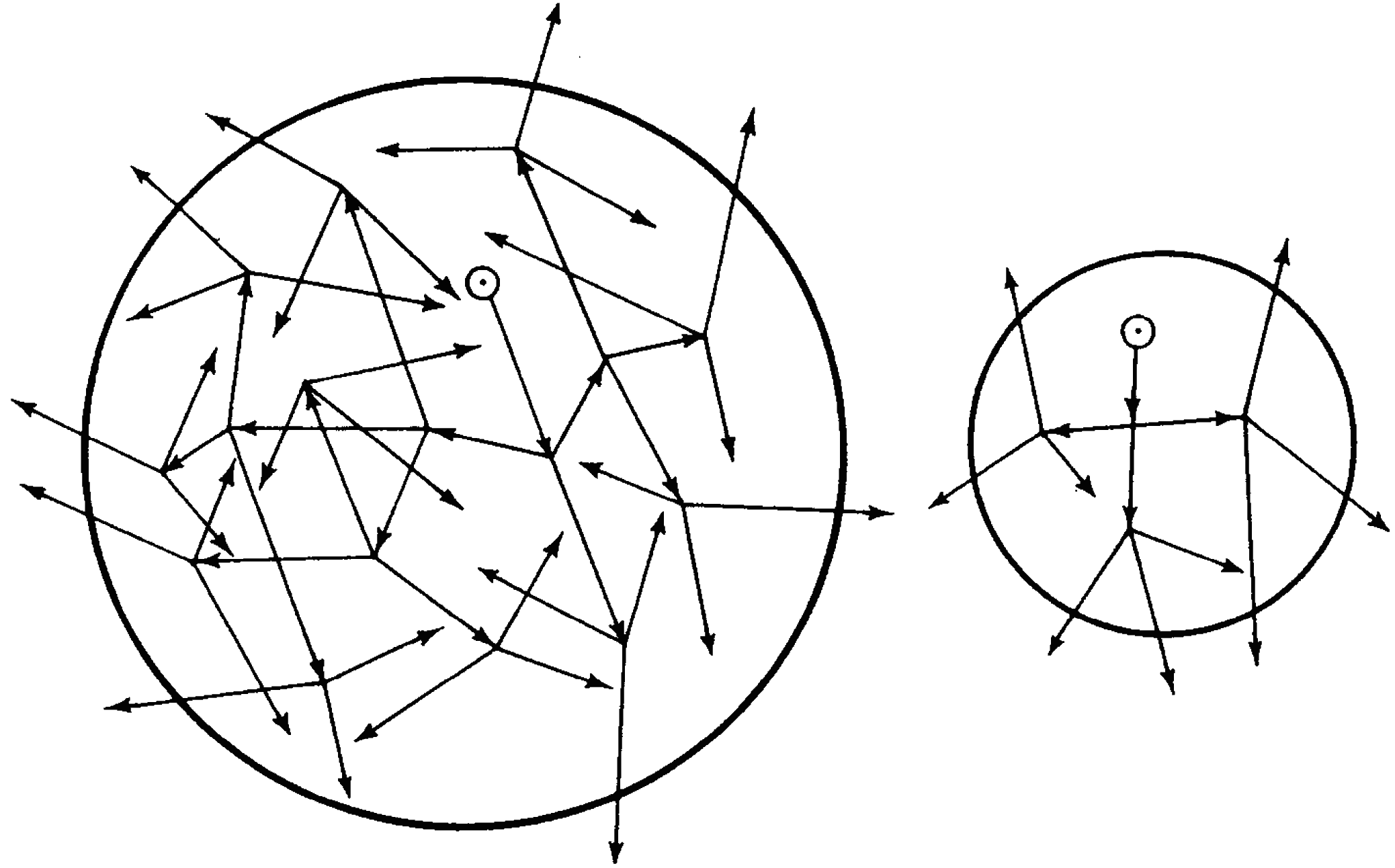
1.49 If the quantity of a fissionable isotope of uranium (or plutonium) is such that the ratio of the surface area to the mass is large, the proportion of neutrons lost by escape will be so great that the propagation of a nuclear fission chain, and hence the production of an explosion, will not be possible. Such a quantity of material is said to be “subcritical.” But as the mass of the piece of uranium (or plutonium) is increased (or the volume is decreased by compression) and the relative loss of neutrons is thereby decreased, a point is reached at which the chain reaction can become self-sustaining. This is referred to as the “critical mass” of the fissionable material under the existing conditions.
1.50 For a nuclear explosion to take place, the weapon must thus contain a sufficient amount of a fissionable uranium (or plutonium) isotope for the critical mass to be exceeded. Actually, the critical mass depends, among other things, on the shape of the material, its composition and density (or compression), and the presence of impurities which can remove neutrons in non-fission reactions. By surrounding the fissionable material with a suitable neutron “reflector,” the loss of neutrons by escape can be reduced, and the critical mass can thus be decreased. Moreover, elements of high density, which make good reflectors for neutrons of high energy, provide inertia, thereby delaying expansion of the exploding material. The action of the reflector is then like the familiar tamping in blasting operations. As a consequence of its neutron reflecting and inertial properties, the “tamper” permits the fissionable material in a nuclear weapon to be used more efficiently.
ATTAINMENT OF CRITICAL MASS IN A WEAPON
1.51 Because of the presence of stray neutrons in the atmosphere or the possibility of their being generated in various ways, a quantity of a suitable isotope of uranium (or plutonium) exceeding the critical mass would be likely to melt or possibly explode. It is necessary, therefore, that before detonation, a nuclear weapon should contain no piece of fissionable material that is as large as the critical mass for the given conditions. In order to produce an explosion, the material must then be made “supercritical,” i.e., larger than the critical mass, in a time so short as to preclude a subexplosive change in the configuration, such as by melting.
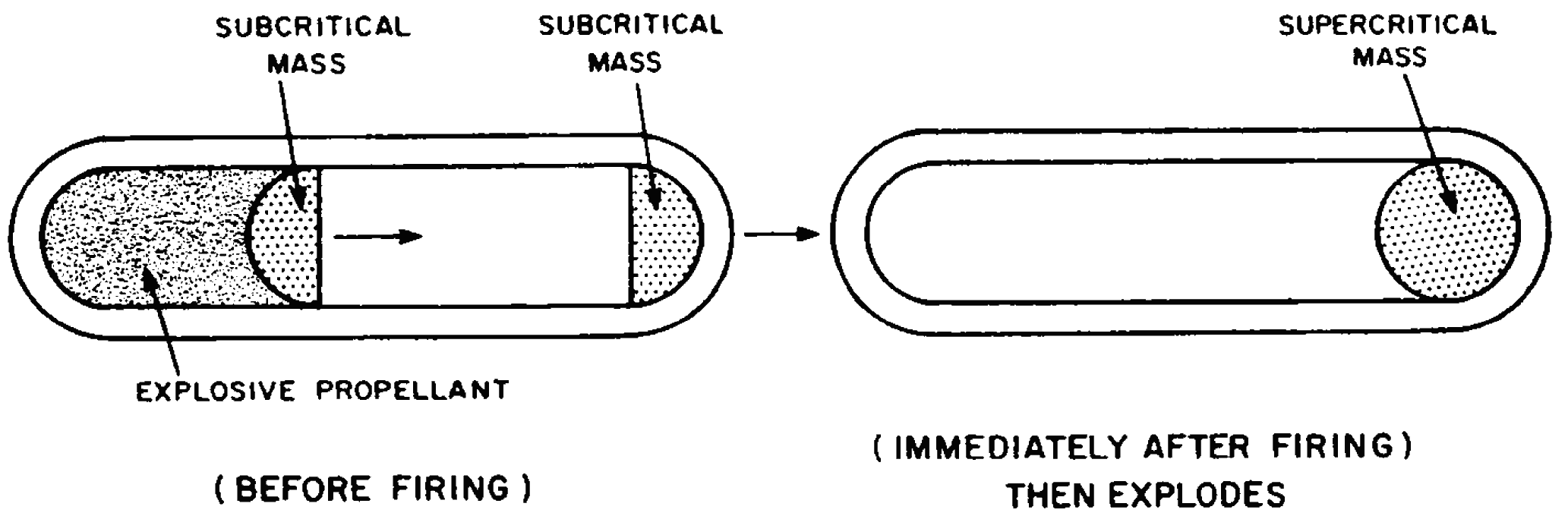
1.52 Two general methods have been described for bringing about a nuclear explosion, that is to say, for quickly converting a subcritical system into a supercritical one. In the first method, two or more pieces of fissionable material, each less than a critical mass, are brought together very rapidly in order to form one piece that exceeds the critical mass (Fig. 1.52). This may be achieved in some kind of gun-barrel device, in which an explosive propellant is used to blow one subcritical piece of fissionable material from the breech end of the gun into another subcritical piece firmly held in the muzzle end.
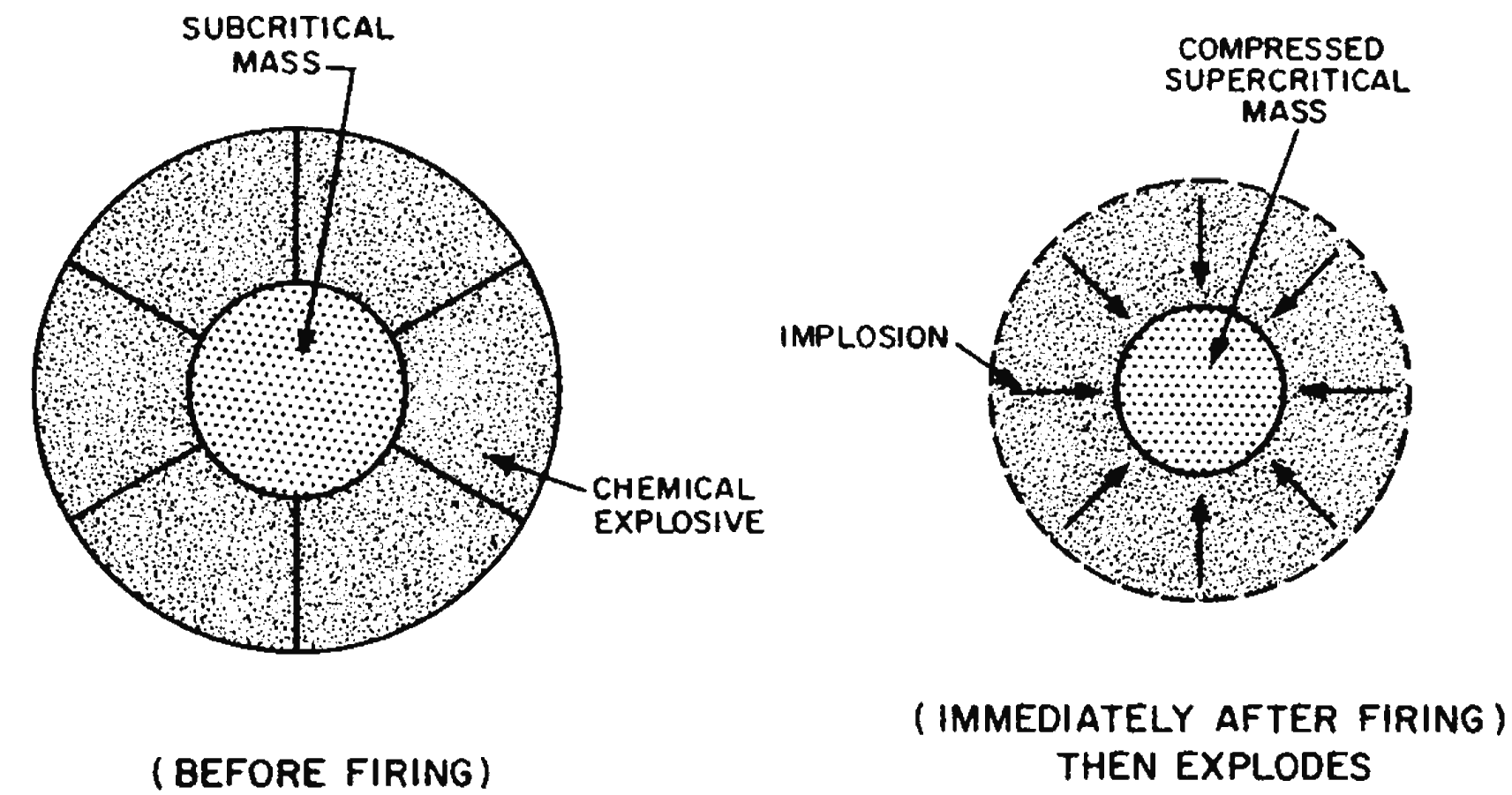
1.53 The second method makes use of the fact that when a subcritical quantity of an appropriate isotope of uranium (or plutonium) is strongly compressed, it can become critical or supercritical as indicated above. The compression may be achieved by means of a spherical arrangement of specially fabricated shapes (lenses) of ordinary high explosive. In a hole in the center of this system is placed a subcritical sphere of fissionable material. When the high-explosive lens system is set off, by means of a detonator on the outside of each lens, an inwardly-directed spherical “implosion” wave is produced. A similar wave can be realized without lenses by detonating a large number of points distributed over a spherical surface. When the implosion wave reaches the sphere of uranium (or plutonium), it causes the latter to be compressed and become supercritical (Fig. 1.53). The introduction of neutrons from a suitable source can then initiate a chain reaction leading to an explosion.
TIME SCALE OF A FISSION EXPLOSION
1.54 An interesting insight into the rate at which the energy is released in a fission explosion can be obtained by treating the fission chain as a series of “generations.” Suppose that a certain number of neutrons are present initially and that these are captured by fissionable nuclei; then, in the fission process other neutrons are released. These neutrons, are, in turn, captured by fissionable nuclei and produce more neutrons, and so on. Each stage of the fission chain is regarded as a generation, and the “generation time” is the average time interval between successive generations. The time required for the actual fission of a nucleus is extremely short and most of the neutrons are emitted promptly. Consequently, the generation time is essentially equal to the average time elapsing between the release of a neutron and its subsequent capture by a fissionable nucleus. This time depends, among other things, on the energy (or speed) of the neutron, and if most of the neutrons are of fairly high energy, usually referred to as “fast neutrons,” the generation time is about a one-hundred-millionth part (10-8) of a second, i.e., 0.01 microsecond.4
1.55 It was mentioned earlier that not all the fission neutrons are available for maintaining the fission chain because some are lost by escape and by removal in nonfission reactions. Suppose that when a nucleus captures a neutron and suffers fission f neutrons are released; let l be the average number of neutrons lost, in one way or another, for each fission. There will thus be f – l neutrons available to carry on the fission chain. If there are N neutrons present at any instant, then as a result of their capture by fissionable nuclei N(f−l) neutrons will be produced at the end of one generation; hence, the increase in the number of neutrons per generation is N(f−l)−N or N(f−l−1). For convenience, the quantity f−l−1, that is, the increase in neutrons per fission, will be represented by x. If g is the generation time, then the rate at which the number of neutrons increases is given by
\[ \begin{align} \text{Rate of neutron increase}\\ \\ dN/dt = 𝑁x/g. \end{align} \]The solution of this equation is
\[ N = N_{0} e^{xt/g}, \] where N0 is the number of neutrons present initially and N is the number at a time t later. The fraction t/g is the number of generations which have elapsed during the time t, and if this is represented by n, it follows that1.56 If the value of x is known, equation (1.55.1) can be used to calculate either the neutron population after any prescribed number of generations in the fission chain, or, alternatively, the generations required to attain a particular number of neutrons. For uranium-235, f is about 2.5, l may be taken to be roughly 0.5, so that x, which is equal to f−l−1, is close to unity; hence, equation (1.55.1) may be written as
1.57 According to the data in Table 1.45, it would need 1.45 × 1022 fissions, and hence the same number of neutrons, to produce 0.1 kiloton equivalent of energy. If the fission chain is initiated by one neutron, so that N0 is 1, it follows from equation (1.56.1) that it would take approximately 51 generations to produce the necessary number of neutrons. Similarly, to release 100 kilotons of energy would require 1.45×1025 neutrons and this number would be attained in about 58 generations. It is seen, therefore, that 99.9 percent of the energy of a 100-kiloton fission explosion is released during the last 7 generations, that is, in a period of roughly 0.07 microsecond. Clearly, most of the fission energy is released in an extremely short time period. The same conclusion is reached for any value of the fission explosion energy.
1.58 In 50 generations or so, i.e., roughly half microsecond, after the initiation of the fission chain, so much energy will have been released—about 1011 calories—that extremely high temperatures will be attained. Consequently, in spite of the restraining effect of the tamper (§ 1.50) and the weapon casing, the mass of fissionable material will begin to expand rapidly. The time at which this expansion commences is called the “explosion time.” Since the expansion permits neutrons to escape more readily, the mass becomes subcritical and the self-sustaining chain reaction soon ends. An appreciable proportion of the fissionable material remains unchanged and some fissions will continue as a result of neutron capture, but the amount of energy released at this stage is relatively small.
1.59 To summarize the foregoing discussion, it may be stated that because the fission process is accompanied by the instantaneous liberation of neutrons, it is possible, in principle to produce a self-sustaining chain reaction accompanied by the rapid release of large amounts of energy. As a result, a few pounds of fissionable material can be made to liberate, within a very small fraction of a second, as much energy as the explosion of many thousands of tons of TNT. This is the basic principle of nuclear fission weapons.
FISSION PRODUCTS
1.60 Many different, initial fission product nuclei, i.e., fission fragments, are formed when uranium or plutonium nuclei capture neutrons and suffer fission. There are 40 or so different ways in which the nuclei can split up when fission occurs; hence about 80 different fragments are produced. The nature and proportions of the fission fragment nuclei vary to some extent, depending on the particular substance undergoing fission and on the energy of the neutrons causing fission. For example, when uranium-238 undergoes fission as a result of the capture of neutrons of very high energy released in certain fusion reactions (§ 1.72), the products are somewhat different, especially in their relative amounts, from those formed from uranium-235 by ordinary fission neutrons.
1.61 Regardless of their origin, most, if not all, of the approximately 80 fission fragments are the nuclei of radioactive forms (radioisotopes) of well-known, lighter elements. The radioactivity is usually manifested by the emission of negatively charged beta particles (§ 1.29). This is frequently, although not always, accompanied by gamma radiation, which serves to carry off excess energy. In a few special cases, gamma radiation only is emitted.
1.62 As a result of the expulsion of a beta particle, the nucleus of a radioactive substance is changed into that of another element, sometimes called the “decay product.” In the case of the fission fragments, the decay products are generally also radioactive, and these in tum may decay with the emission of beta particles and gamma rays. On the average there are about four stages of radioactivity for each fission fragment before a stable (nonradioactive) nucleus is formed. Because of the large number of different ways in which fission can occur and the several stages of decay involved, the fission product mixture becomes very complex.5 More than 300 different isotopes of 36 light elements, from zinc to terbium, have been identified among the fission products.
1.63 The rate of radioactive change, i.e., the rate of emission of beta particles and gamma radiation, is usually expressed by means of the “half-life” of the radionuclide (§ 1.30) involved. This is defined as the time required for the radioactivity of a given quantity of a particular nuclide to decrease (or decay) to half of its original value. Each individual radionuclide has a definite half-life which is independent of its state or its amount. The half-lives of the fission products have been found to range from a small fraction of a second to something like a million years.
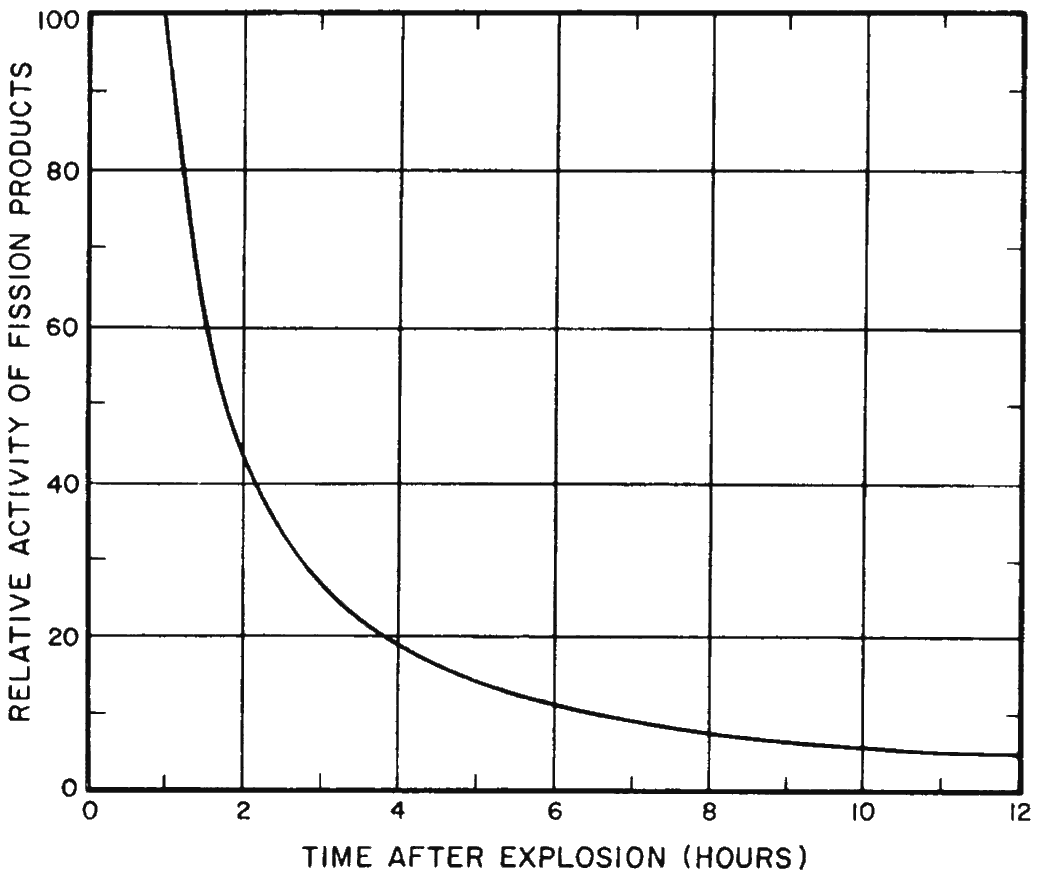
1.64 Although every radionuclide present among the fission products is known to have a definite half-life, the mixture formed after a nuclear explosion is so complex that it is not possible to represent the decay as a whole in terms of a half-life. Nevertheless, it has been found that the decrease in the total radiation intensity from the fission products can be calculated approximately by means of a fairly simple formula. This will be given and discussed in Chapter IX, but the general nature of the decay rate of fission products, based on this formula, will be apparent from Fig. 1.64. The residual radioactivity from the fission products at 1 hour after a nuclear detonation is taken as 100 and the subsequent decrease with time is indicated by the curve. It is seen that at 7 hours after the explosion, the fission product activity will have decreased to about one-tenth (10 percent) of its amount at 1 hour. Within approximately 2 days, the activity will have decreased to 1 percent of the 1-hour value.
1.65 In addition to the beta-particle and gamma-ray activity due to the fission products, there is another kind of residual radioactivity that should be mentioned. This is the activity of the fissionable material, part of which, as noted in § 1.58, remains after the explosion. The fissionable uranium and plutonium isotopes are radioactive, and their activity consists in the emission of what are called “alpha particles.” These are a form of nuclear radiation, since they are expelled from atomic nuclei; but they differ from the beta particles arising from the fission products in being much heavier and carrying a positive electrical charge. Alpha particles are, in fact, identical with the nuclei of helium atoms.
1.66 Because of their greater mass and charge, alpha particles are much less penetrating than beta particles or gamma rays of the same energy. Thus, very few alpha particles from radioactive sources can travel more than 1 to 3 inches in air before being stopped. It is doubtful that these particles can get through the unbroken skin, and they certainly cannot penetrate clothing. Consequently, the uranium (or plutonium) present in the weapon residues does not constitute a hazard if the latter are outside the body. However, if plutonium enters the body by ingestion, through skin abrasions, or particularly through inhalation, the effects may be serious.
FUSION (THERMONUCLEAR) REACTIONS
1.67 Energy production in the sun and stars is undoubtedly due to fusion reactions involving the nuclei of various light (low atomic weight) atoms. From experiments made in laboratories with charged-particle accelerators, it was concluded that the fusion of isotopes of hydrogen was possible. This element is known to exist in three isotopic forms, in which the nuclei have mass numbers (§ 1.10) of 1, 2, and 3, respectively. These are generally referred to as hydrogen (1H), deuterium (2H or D), and tritium (3H or T). All the nuclei carry a single positive charge, i.e., they all contain one proton, but they differ in the number of neutrons. The lightest (1H) nuclei (or protons) contain no neutrons; deuterium (D) nuclei contain one neutron, and tritium (T) nuclei contain two neutrons.
1.68 Several different fusion reactions have been observed between the nuclei of the three hydrogen isotopes, involving either two similar or two different nuclei. In order to make these reactions occur to an appreciable extent, the nuclei must have high energies. One way in which this energy can be supplied is to raise the temperature to very high levels. In these circumstances the fusion processes are referred to as “thermonuclear reactions,” as mentioned in § 1.17.
1.69 Four thermonuclear fusion reactions appear to be of interest for the production of energy because they are expected to occur sufficiently rapidly at realizable temperatures; these are:
D + D = 3He + n + 3.2 MeV D + D = T + 1H + 4.0 MeV T + D = 4He + n + 17. 6 MeV T + T = 4He + 2n + 11.3 MeV,
where He is the symbol for helium and n (mass = 1) represents a neutron. The energy liberated in each case is given in million electron volt (MeV) units. The first two of these reactions occur with almost equal probability at the temperatures associated with nuclear explosions (several tens of million degrees Kelvin), whereas the third reaction has a much higher probability and the fourth a much lower probability. Thus, a valid comparison of the energy released in fusion reactions with that produced in fission can be made by noting that, as a result of the first three reactions given above, five deuterium nuclei, with a total mass of 10 units, will liberate 24.8 MeV upon fusion. On the other hand, in the fission process, e.g., of uranium-235, a mass of 235 units will produce a total of about 200 MeV of energy (§ 1.43). Weight for weight, therefore, the fusion of deuterium nuclei would produce nearly three times as much energy as the fission of uranium or plutonium.
1.70 Another reaction of thermonuclear weapons interest, with tritium as a product, is
\[ ^{6}\text{Li} + n \to ^{4}\text{He} + ^{3}\text{T} + 4.8 \text{MeV}, \]where 6Li represents the lithium-6 isotope, which makes up about 7.4 percent of natural lithium. Other reactions can occur with lithium-6 or the more abundant isotope lithium-7 and various particles produced in the weapon. However, the reaction shown above is of most interest for two reasons: (1) it has a high probability of occurrence and (2) if the lithium is placed in the weapon in the form of the compound lithium deuteride (LiD), the tritium formed in the reaction has a high probability of interacting with the deuterium. Large amounts of energy are thus released by the third reaction in § 1.69, and additional neutrons are produced to react with lithium-6.
1.71 In order to make the nuclear fusion reactions take place at the required rate, temperatures of the order of several tens of million degrees are necessary. The only practical way in which such temperatures can be obtained on earth is by means of a fission explosion. Consequently, by combining a quantity of deuterium or lithium deuteride (or a mixture of deuterium and tritium) with a fission device, it should be possible to initiate one or more of the thermonuclear fusion reactions given above. If these reactions, accompanied by energy evolution, can be propagated rapidly through a volume of the hydrogen isotope (or isotopes) a thermonuclear explosion may be realized.
1.72 It will be observed that in three of the fusion reactions given in § 1.69, neutrons are produced. Because of their small mass, these neutrons carry off most of the reaction energy; consequently, they have sufficient energy to cause fission of uranium-238 nuclei. As stated earlier, this process requires neutrons of high energy. It is possible, therefore, to make use of the thermonuclear neutrons by surrounding the fusion weapon with a blanket of ordinary uranium. The high-energy neutrons are then captured by uranium-238 nuclei; the latter undergo fission, thereby contributing to the overall energy yield of the explosion, and also to the residual nuclear radiation arising from the fission products. On the average, the energy released in the explosion of a thermonuclear weapon originates in roughly equal amounts from fission and fusion processes,although there may be variations in individual cases. In “boosted” fission weapons, thermonuclear neutrons serve to enhance the fission process; energy released in the thermonuclear reaction is then a small fraction of the total energy yield.
THERMAL RADIATION
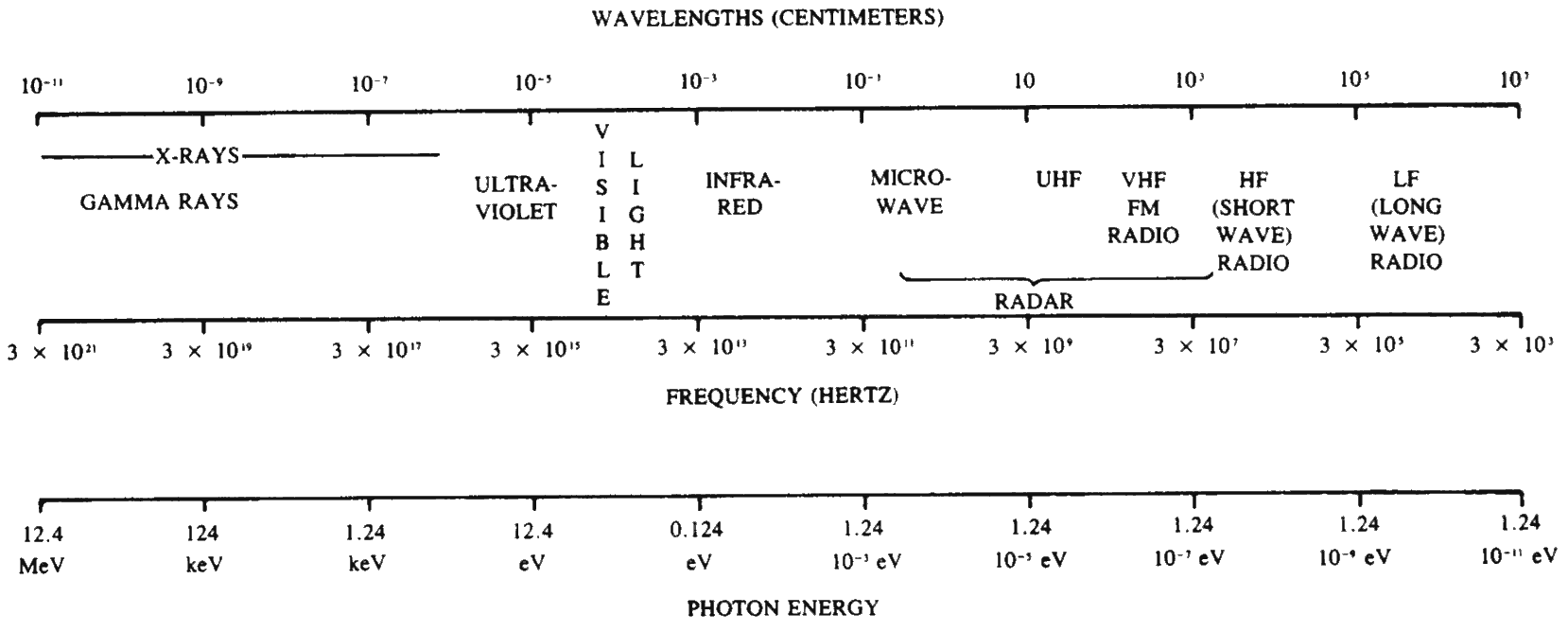
1.73 The observed phenomena associated with a nuclear explosion and the effects on people and materials are largely determined by the thermal radiation and its interaction with the surroundings. It is desirable, therefore, to consider the nature of these radiations somewhat further. Thermal radiations belong in the broad category of what are known as “electromagnetic radiations.” These are a kind of wave motion resulting from oscillating electric charges and their associated magnetic fields. Ordinary visible light is the most familiar kind of electromagnetic radiation, and all such radiations travel through the air (or, more exactly, a vacuum) at the same velocity, namely, the velocity of light, 186,000 miles per second. Electromagnetic radiations range from the very short wavelength (or very high frequency) gamma rays (§ 1.28) and X rays, through the invisible ultraviolet to the visible region, and then to the infrared and radar and radio waves of relatively long wavelength (and low frequency).
1.74 The approximate wavelength and frequency regions occupied by the different kinds of electromagnetic radiations are indicated in Fig. 1.74. The wavelength λ in centimeters and the frequency v in hertz, i.e., in waves (or cycles) per second, are related by λv = c, where c is the velocity of light, 3.00×1010 cm per second. According to Planck’s theory, the energy of the corresponding “quantum” (or unit) of energy, carried by the “photon,” i.e., the postulated particle (or atom) of radiation, is given by
where h is a universal constant equal to 6.62×10-27 erg-second. The energy quantum values for the various electromagnetic radiations are included in Fig. . 74; the results are expressed either in MeV, i.e., million electron volt, in keV, i.e., kilo (or thousand) electron volt, or in eV, i.e., electron volt, units. These are obtained from equation (1.74.1) by writing it in the form
It is seen that the energy of the radiations decreases from left to right in the figure, i.e., as the wavelength increases and the frequency decreases.
1.75 The (thermal) radiation energy density for matter in temperature equilibrium is given by
\[ E (\text{radiation}) = 7.6×10^{-15}T^{4} \text{ ergs/cm}^{3}, \]where T is the temperature in degrees Kelvin. At the temperature of a conventional chemical explosion, e.g., 5,000°K, the radiation energy density is then less than 1 erg/cm3, compared with roughly 108 ergs/cm3 for the material energy, i.e., kinetic energy and internal (electronic, vibrational, and rotational) energy. Hence, as indicated in § 1.23, the radiation energy is a very small proportion of the total energy. In a nuclear explosion, on the other hand, where temperatures of several tens of million degrees are reached, the radiation energy density will be of the order of 1016 ergs/cm3, whereas the material energy is in the range of 1014 to 1015 ergs/cm3 . It has been estimated that in a nuclear explosion some 80 percent of the total energy may be present initially as thermal radiation energy.
1.76 Not only does the radiation energy density increase with temperature but the rate of its emission as thermal radiation increases correspondingly. For materials at temperatures of a few thousand degrees Kelvin, the energy is radiated slowly, with the greatest part in the ultraviolet, visible, and infrared regions of the electromagnetic spectrum (Fig. 1.74). At the temperatures of a nuclear explosion, however, not only is the radiation energy emitted very rapidly, but most of this energy is in the spectral region with wavelengths shorter than the ultraviolet.
1.77 When a nuclear weapon explodes, temperature equilibrium is rapidly established in the residual material. Within about one microsecond after the explosion, some 70 to 80 percent of the explosion energy, as defined in § 1.27, is emitted as primary thermal radiation, most of which consists of soft X rays.6 Almost all of the rest of the energy is in the form of kinetic energy of the weapon debris at this time. The interaction of the primary thermal radiation and the debris particles with the surroundings will vary with the altitude of burst and will determine the ultimate partition of energy between the thermal radiation received at a distance and shock.
1.78 When a nuclear detonation occurs in the air, where the atmospheric pressure (and density) is near to sea-level conditions, the soft X rays in the primary thermal radiation are completely absorbed within a distance of a few feet. Some of the radiations are degraded to lower energies, e.g., into the ultraviolet region, but most of the energy of the primary thermal radiation serves to heat the air immediately surrounding the nuclear burst. It is in this manner that the fireball is formed. Part of the energy is then reradiated at a lower temperature from the fireball and the remainder is converted into shock (or blast) energy (see Chapter II). This explains why only about 35 to 45 percent of the fission energy from an air burst is received as thermal radiation energy at a distance, although the primary thermal radiation may constitute as much as 70 to 80 percent of the total. Furthermore, because the secondary thermal radiation is emitted at a lower temperature, it lies mainly in the region of the spectrum with longer wavelengths (lower photon energies), i.e., ultraviolet, visible, and infrared7 (see Chapter VII).
1.79 In the event of a burst at high altitudes, where the air density is low, the soft X rays travel long distances before they are degraded and absorbed. At this stage, the available energy is spread throughout such a large volume (and mass) that most of the atoms and molecules in the air cannot get very hot. Although the total energy emitted as thermal radiation in a high-altitude explosion is greater than for an air burst closer to sea level, about half is reradiated so slowly by the heated air that it has no great significance as a cause of damage. The remainder, however, is radiated very much more rapidly, i.e., in a shorter time interval, than is the case at lower altitudes. A shock wave is generated from a high-altitude burst, but at distances of normal practical interest it produces a smaller pressure increase than from an air burst of the same yield. These matters are treated more fully in Chapter II.
BIBLIOGRAPHY
- , “Review of Nuclear Weapons Effects,”Annual Review of Nuclear Science, 18, 153 (1968).
- , “Fission Product Decay Chains: Schematics with Branching Fractions, Half-Lives, and Literature References,” U.S. Naval Radiological Defense Laboratory, June 1967, USNRDL–TR–67–111.
- , “Calculated Abundances and Activities of the Products of High Energy Neutron Fission of Uranium-238,” Defense Atomic Support Agency, May 1959, DASA 525.
- , “Sourcebook on Atomic Energy,” D. Van Nostrand Co., Inc., Third Edition, 1967.
- , “Nucleonics Fundamentals,” McGraw-Hill Book Co., Inc., 1959, Chapter 14.
- , “Men and Atoms,” Simon and Schuster, Inc., 1959.
- , “An Introduction to Fission Explosions,” University of California, Lawrence Radiation Laboratory, Livermore, July 1969, UCID–15554.
- , “Atomic Energy for Military Purposes,” Princeton University Press, 1945.
- “Estimated Total Chain and Independent Fission Yields for Several Neutron-Induced Fission Processes,” U.S. Naval Radiological Defense Laboratory, March 1963, USNRDL–TR–633.
ENDNOTES
- 1 The terms “nuclear” and "atomic” may be used interchangeably so far as weapons, explosions, and energy are concerned, but “nuclear” is preferred for the reason given in § 1.11. [ref. § 1.01] X
- 2 The remaining (more technical) sections of this chapter may be omitted without loss of continuity. [ref. Section 2] X
- 3 The majority of the experimental and theoretical values of the explosive energy released by TNT range from 900 to 1,100 calories per gram. At one time, there was some uncertainty as to whether the term “kiloton” of TNT referred to a short kiloton (2×106 pounds), a metric kiloton (2.205×106 pounds), or a long kiloton (2.24×106 pounds). In order to avoid ambiguity, it was agreed that the term “kiloton” would refer to the release of 1012 calories of explosive energy. This is equivalent to 1 short kiloton of TNT if the energy release is 1,102 calories per gram or to 1 long kiloton if the energy is 984 calories per gram of TNT. [ref. § 1.45] X
- 4 A microsecond is a one-millionth part of a second, i.e., 10-6 second; a hundredth of a microsecond, i.e., 10-8 second, is often called a “shake.” The generation time in fission by fast neutrons is thus roughly 1 shake. [ref. § 1.54] X
- 5 The general term “fission products” is used to describe this complex mixture. [ref. § 1.62] X
- 6 X rays are frequently distinguished as “hard” or “soft.” The latter have longer wavelengths and lower energies, and they are more easily absorbed than hard X rays. They are, nevertheless, radiations of high energy compared with ultraviolet or visible light. [ref. § 1.77] X
- 7 It is sometimes referred to as the “prompt thermal radiation” because only that which is received within a few seconds of the explosion is significant as a hazard. [ref. § 1.78] X