Atomic Energy for Military Purposes (The Smyth Report)
CHAPTER I. INTRODUCTION
1.1. The purpose of this report is to describe the scientific and technical developments in this country since 1940 directed toward the military use of energy from atomic nuclei. Although not written as a "popular" account of the subject, this report is intended to be intelligible to scientists and engineers generally and to other college graduates with a good grounding in physics and chemistry. The equivalence of mass and energy is chosen as the guiding principle in the presentation of the background material of the "Introduction."
THE CONSERVATION OF MASS AND OF ENERGY
1.2. There are two principles that have been cornerstones of the structure of modern science. The first - that matter can be neither created nor destroyed but only altered in form - was enunciated in the eighteenth century and is familiar to every student of chemistry; it has led to the principle known as the law of conservation of mass. The second - that energy can be neither created nor destroyed but only altered in form emerged in the nineteenth century and has ever since been the plague of inventors of perpetual-motion machines; it is known as the law of conservation of energy.
1.3. These two principles have constantly guided and disciplined the development and application of science. For all practical purposes they were unaltered and separate until some five years ago. For most practical purposes they still are so, but it is now known that they are, in fact, two phases of a single principle for we have discovered that energy may sometimes be converted into matter and matter into energy. Specifically, such a conversion is observed in the phenomenon of nuclear fission of uranium, a process in which atomic nuclei split into fragments with the release of an enormous amount of energy. The military use of this energy has been the object of the research and production projects described in this report.
THE EQUIVALENCE OF MASS AND ENERGY
1.4. One conclusion that appeared rather early in the development of the theory of relativity was that the inertial mass of a moving body increased as its speed increased. This implied an equivalence between an increase in energy of motion of a body, that is, its kinetic energy, and an increase in its mass. To most practical physicists and engineers this appeared a mathematical fiction of no practical importance. Even Einstein could hardly have foreseen the present applications, but as early as 1905 he did clearly state that mass and energy were equivalent and suggested that proof of this equivalence might be found by the study of radioactive substances. He concluded that the amount of energy, E, equivalent to a mass, m, was given by the equation
E = mc2
where c is the velocity of light. If this is stated in actual numbers, its startling character is apparent. It shows that one kilogram (2.2 pounds) of matter, if converted entirely into energy, would give 25 billion kilowatt hours of energy. This is equal to the energy that would be generated by the total electric power industry in the United States (as of 1939) running for approximately two months. Compare this fantastic figure with the 8.5 kilowatt hours of heat energy which may be produced by burning an equal amount of coal.
1.5. The extreme size of this conversion figure was interesting in several respects. In the first place, it explained why the equivalence of mass and energy was never observed in ordinary chemical combustion. We now believe that the heat given off in such a combustion has mass associated with it, but this mass is so small that it cannot he detected by the most sensitive balances available. (It is of the order of a few billionths of a gram per mole.) In the second place, it was made clear that no appreciable quantities of matter were being converted into energy in any familiar terrestrial processes, since no such large sources of energy were known. Further, the possibility of initiating or controlling such a conversion in any practical way seemed very remote. Finally, the very size of the conversion factor opened a magnificent field of speculation to philosophers, physicists, engineers, and comic-strip artists. For twenty-five years such speculation was unsupported by direct experimental evidence, but beginning about 1930 such evidence began to appear in rapidly increasing quantity. Before discussing such evidence and the practical partial conversion of matter into energy that is our main theme, we shall review the foundations of atomic and nuclear physics. General familiarity with the atomic nature of matter and with the existence of electrons is assumed. Our treatment will be little more than an outline which may be elaborated by reference to books such as Pollard and Davidson's Applied Nuclear Physics and Stranathan's The "Particles" of Modern Physics.
RADIOACTIVITY AND ATOMIC STRUCTURE
1.6. First discovered by H. Becquerel in 1896 and subsequently studied by Pierre and Marie Curie, E. Rutherford, and many others, the phenomena of radioactivity have played leading roles in the discovery of the general laws of atomic structure and in the verification of the equivalence of mass and energy.
IONIZATION BY RADIOACTIVE SUBSTANCES
1.7. The first phenomenon of radioactivity observed was the blackening of photographic plates by uranium minerals. Although this effect is still used to some extent in research on radioactivity, the property of radioactive substances that is of greatest scientific value is their ability to ionise gases. Under normal conditions air and other gases do not conduct electricity - otherwise power lines and electrical machines would not operate in the open as they do. But under some circumstances the molecules of air are broken apart into positively and negatively charged fragments, called ions. Air thus ionized does conduct electricity. Within a few months after the first discovery of radioactivity Becquerel found that uranium had the power to ionize air. Specifically he found that the charge on an electroscope would leak away rapidly through the air if some uranium salts were placed near it. (The same thing would happen to a storage battery if sufficient radioactive material were placed near by.) Ever since that time the rate of discharge of an electroscope has served as a measure of intensity of radioactivity. Furthermore, nearly all present-day instruments for studying radioactive phenomena depend on this ionization effect directly or indirectly. An elementary account of such instruments, notably electroscopes, Geiger-Müller counters, ionization chambers, and Wilson cloud chambers is given in Appendix 1.
THE DIFFERENT RADIATIONS OR PARTICLES
1.8. Evidence that different radioactive substances differ in their ionizing power both in kind and in intensity indicates that there are differences in the "radiations" emitted. Some of the radiations are much more penetrating than others; consequently, two radioactive samples having the same effect on an "unshielded" electroscope may have very different effects if the electroscope is "shielded," i.e., if screens are interposed between the sample and the electroscope. These screens are said to absorb the radiation.
1.9. Studies of absorption and other phenomena have shown that in fact there are three types of "radiation" given off by radioactive substances. There are alpha particles, which are high-speed ionized helium atoms (actually the nuclei of helium atoms), beta particles, which are high-speed electrons, and gamma rays, which are electromagnetic radiations similar to X-rays. Of these only the gamma rays are properly called radiations, and even these act very much like particles because of their short wavelength. Such a "particle" or quantum of gamma radiation is called a photon. In general, the gamma rays are very penetrating, the alpha and beta rays less so. Even though the alpha and beta rays are not very penetrating, they have enormous kinetic energies for particles of atomic size, energies thousands of times greater than the kinetic energies which the molecules of a gas have by reason of their thermal motion, and thousands of times greater than the energy changes per atom in chemical reactions. It was for this reason that Einstein suggested that studies of radioactivity might show the equivalence of mass and energy.
THE ATOM
1.10. Before considering what types of atoms emit alpha, beta and gamma rays, and before discussing the laws that govern such emission, we shall describe the current ideas on how atoms are constructed, ideas based partly on the study of radioactivity.
1.11. According to our present view every atom consists of a small heavy nucleus approximately 10-12 cm in diameter surrounded by a largely empty region 10-8 cm in diameter in which electrons move somewhat like planets about the sun. The nucleus carries an integral number of positive charges, each 1.6 × 10-19 coulombs in size. (See Appendix 2 for a discussion of units.) Each electron carries one negative charge of this same size, and the number of electrons circulating around the nucleus is equal to the number of positive charges on the nucleus so that the atom as a whole has a net charge of zero.
1.12. Atomic number and Electronic Structure. The number of positive charges in the nucleus is called the atomic number, Z. It determines the number of electrons in the extranuclear structure, and this in turn determines the chemical properties of the atom. Thus all the atoms of a given chemical element have the same atomic number, and conversely all atoms having the same atomic number are atoms of the same element regardless of possible differences in their nuclear structure. The extranuclear electrons in an atom arrange themselves in successive shells according to well-established laws. Optical spectra arise from disturbances in the outer parts of this electron structure; X-rays arise from disturbances of the electrons close to the nucleus. The chemical properties of an atom depend on the outermost electrons, and the formation of chemical compounds is accompanied by minor rearrangements of these electronic structures. Consequently, when energy is obtained by oxidation, combustion, explosion, or other chemical processes, it is obtained at the expense of these structures so that the arrangement of the electrons in the products of the process must be one of lowered energy content. (Presumably the total mass of these products is correspondingly lower but not detectably so.) The atomic nuclei are not affected by any chemical process.
1.13. Mass Number. Not only is the positive charge on a nucleus always an integral number of electronic charges, but the mass of the nucleus is always approximately a whole number times a fundamental unit of mass which is almost the mass of a proton, the nucleus of a hydrogen atom. (See Appendix 2.) This whole number is called the mass number, A, and is always at least twice as great as the atomic number except in the cases of hydrogen and a rare isotope of helium. Since the mass of a proton is about 1,800 times that of an electron, the mass of the nucleus is very nearly the whole mass of the atom.
1.14. Isotopes and Isobars. Two species of atoms having the same atomic number but different mass numbers are called isotopes. They are chemically identical, being merely two species of the same chemical element. If two species of atoms have the same mass number but different atomic numbers, they are called isobars and represent two different chemical elements.
RADIOACTIVITY AND NUCLEAR CHANGE
1.15. If an atom emits an alpha particle (which has an atomic number of two and a mass of four), it becomes an atom of a different element with an atomic number lower by two and a mass number lower by four. The emission by a nucleus of a beta particle increases the atomic number by one and leaves the mass number unaltered. In some cases. these changes are accompanied by the emission of gamma rays. Elements which spontaneously change or "disintegrate" in these ways are unstable and are described as being "radioactive." The only natural elements which exhibit this property of emitting alpha or beta particles are (with a few minor exceptions) those of very high atomic numbers and mass numbers, such as uranium, thorium, radium, and actinium, i.e., those known to have the most complicated nuclear structures.
HALF-LIVES; THE RADIOACTIVE SERIES
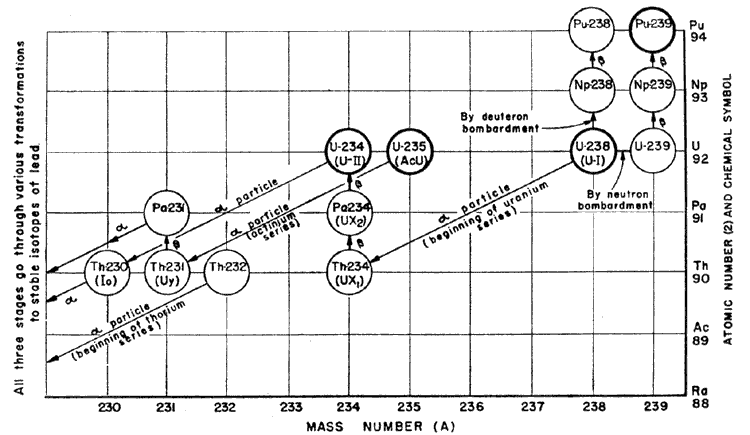
1.16. All the atoms of a particular radioactive species have the same probability of disintegrating in a given time, so that an appreciable sample of radioactive material, containing many millions of atoms, always changes or "disintegrates" at the same rate. This rate at which the material changes is expressed in terms of the "half-life", the time required for one half the atoms initially present to disintegrate, which evidently is constant for any particular atomic species. Half-lives of radioactive materials range from fractions of a second for the most unstable to billions of years for those which are only slightly unstable. Often, the "daughter" nucleus like its radioactive "parent" is itself radioactive and so on down the line for several successive generations of nuclei until a stable one is finally reached. There are three such families or series comprising all together about forty different radioactive species. The radium series starts from one isotope of uranium, the actinium series from another isotope of uranium, and the thorium series from thorium. The final product of each series, after ten or twelve successive emissions of alpha and beta particles, is a stable isotope of lead.
FIRST DEMONSTRATION OF ARTIFICIAL NUCLEAR DISINTEGRATION
1.17. Before 1919 no one had succeeded in disturbing the stability of ordinary nuclei or affecting the disintegration rates of those that were naturally radioactive. In 1919 Rutherford showed that high-energy alpha particles could cause an alteration in the nucleus of an ordinary element. Specifically he succeeded in changing a few atoms of nitrogen into atoms of oxygen by bombarding them with alpha particles. The process involved may be written as
He4 + N14 → 017 + H1
meaning that a helium nucleus of mass number 4 (an alpha particle) striking a nitrogen nucleus of mass number 14 produces an oxygen nucleus of mass number 17 and a hydrogen nucleus of mass number 1. The hydrogen nucleus, known as the "proton," is of special importance since it has the smallest mass of any nucleus. Although protons do not appear in natural radioactive processes, there is much direct evidence that they can be knocked out of nuclei.
THE NEUTRON
1.18. In the decade following Rutherford's work many similar experiments were performed with similar results. One series of experiments of this type led to the discovery of the neutron, which will be discussed in some detail since the neutron is practically the theme song of this whole project.
1.19. In 1930 W. Bothe and H. Becker in Germany found that if the very energetic natural alpha particles from polonium fell on certain of the light elements, specifically beryllium, boron or lithium, an unusually penetrating radiation was produced. At first this radiation was thought to be gamma radiation although it was more penetrating than any gamma rays known, and the details of experimental results were very difficult to interpret on this basis. The next important contribution was reported in 1932 by Irene Curie and F. Joliot in Paris. They showed that if this unknown radiation fell on paraffin or any other hydrogen containing compound it ejected protons of very high energy. This was not in itself inconsistent with the assumed gamma-ray nature of the new radiation, but detailed quantitative analysis of the data became increasingly difficult to reconcile with such an hypothesis. Finally (later in 1932) J. Chadwick in England performed a series of experiments showing that the gamma-ray hypothesis was untenable. He suggested that in fact the new radiation consisted of uncharged particles of approximately the mass of the proton, and he performed a series of experiments verifying his suggestion. Such uncharged particles are now called neutrons.
1.20. The one characteristic of neutrons which differentiates them from other subatomic particles is the fact that they are uncharged. This property of neutrons delayed their discovery, makes them very penetrating, makes it impossible to observe them directly, and makes them very important as agents in nuclear change. To be sure, an atom in its normal state is also uncharged, but it is ten thousand times larger than a neutron and consists of a complex system of negatively charged electrons widely spaced around a positively charged nucleus. Charged particles (such as protons, electrons, or alpha particles) and electromagnetic radiations (such as gamma rays) lose energy in passing through matter. They exert electric forces which ionize atoms of the material through which they pass. (It is such ionization processes that make the air electrically conducting in the path of electric sparks and lightning flashes.) The energy taken up in ionization equals the energy lost by the charged particle, which slows down, or by the gamma ray, which is absorbed. The neutron, however, is unaffected by such forces; it is affected only by a very short-range force, i.e., a force that comes into play when the neutron comes very close indeed to an atomic nucleus. This is the kind of force that holds a nucleus together in spite of the mutual repulsion of the positive charges in it. Consequently a free neutron goes on its way unchecked until it makes a "head-on" collision with an atomic nucleus. Since nuclei are very small, such collisions occur but rarely and the neutron travels a long way before colliding. In the case of a collision of the "elastic" type, the ordinary laws of momentum apply as they do in the elastic collision of billiard balls. If the nucleus that is struck is heavy, it acquires relatively little speed, but if it is a proton, which is approximately equal in mass to the neutron, it is projected forward with a large fraction of the original speed of the neutron, which is itself correspondingly slowed. Secondary projectiles resulting from these collisions may be detected, for they are charged and produce ionization. The uncharged nature of the neutron makes it not only difficult to detect but difficult to control. Charged particles can be accelerated, decelerated, or deflected by electric or magnetic fields which have no effect on neutrons. Furthermore, free neutrons can be obtained only from nuclear disintegrations; there is no natural supply. The only means we have of controlling free neutrons is to put nuclei in their way so that they will be slowedand deflected or absorbed by collisions. As we shall see, these effects are of the greatest practical importance.
THE POSITRON AND THE DEUTERON
1.21. The year 1932 brought the discovery not only of the neutron but also of the positron. The positron was first observed by C. D. Anderson at the California Institute of Technology. It has the same mass and the same magnitude of charge as the electron, but the charge is positive instead of negative. Except as a particle emitted by artificially radioactive nuclei it is of little interest to us.
1.22. One other major discovery marked the year 1932. H. C. Urey, F. G. Brickwedde, and G. M. Murphy found that hydrogen had an isotope of mass number 2, present in natural hydrogen to one part in 5,000. Because of its special importance this heavy species of hydrogen is given a name of its own, deuterium, and the corresponding nucleus is called the deuteron. Like the alpha particle the deuteron is not one of the fundamental particles but does play an important role in certain processes for producing nuclear disintegration.
NUCLEAR STRUCTURE
1.23. The idea that all elements are made out of a few fundamental particles is an old one. It is now firmly established. We believe that there are three fundamental particles - the neutron, the proton, and the electron. A complete treatise would also discuss the positron, which we have mentioned, the neutrino and the mesotron. The deuteron and alpha particle, which have already been mentioned, are important complex particles.
1.24. According to our present views the nuclei of all atomic species are made up of neutrons and protons. The number of protons is equal to the atomic number, Z. The number of neutrons, N, is equal to the difference between the mass number and the atomic number, or A-Z. There are two sets of forces acting on these particles, ordinary electric coulomb forces of repulsion between the positive charges and very short/range forces between all the particles. These last forces are only partly understood, and we shall not attempt to discuss them. Suffice it to say that combined effects of these attractive and repulsive forces are such that only certain combinations of neutrons and protons are stable. If the neutrons and protons are few in number, stability occurs when their numbers are about equal. For larger nuclei, the proportion of neutrons required for stability is greater. Finally, at the end of the periodic table, where the number of protons is over 90 and the number of neutrons nearly 150, there are no completely stable nuclei. (Some of the heavy nuclei are almost stable as evidenced by very long half-lives.) If an unstable nucleus is formed artificially by adding an extra neutron or proton, eventually a change to a stable form occurs. Strangely enough, this is not accomplished by ejecting a proton or a neutron but by ejecting a positron or an electron; apparently within the nucleus a proton converts itself into a neutron and positron (or a neutron converts itself into a proton and electron), and the light charged particle is ejected. In other words, the mass number remains the same but the atomic number changes. The stability conditions are not very critical so that for a given mass number, i.e., given total number of protons and neutrons, there may be several stable arrangements of protons and neutrons (at most three or five) giving several isobars. For a given atomic number, i.e., given number of protons, conditions can vary still more widely so that some of the heavy elements have as many as ten or twelve stable isotopes. Some two hundred and fifty different stable nuclei have been identified, ranging in mass number from one to two hundred and thirty-eight and in atomic number from one to ninety-two.
1.25. All the statements we have been making are based on experimental evidence. The theory of nuclear forces is still incomplete but it has been developed on quantum-mechanical principles sufficiently to explain not only the above observations but more detailed empirical data on artificial radioactivity and on differences between nuclei with odd and even mass numbers.
ARTIFICIAL RADIOACTIVITY
1.26. We mentioned the emission of positrons or electrons by nuclei seeking stability. Electron emission (beta rays) was already familiar in the study of naturally radioactive substances, but positron emission was not found in the case of such substances. In fact, the general discussion presented above obviously was based in part on information that cannot be presented in this report. We shall, however, give a brief account of the discovery of "artificial" radioactivity and what is now known about it.
1.27. In 1934, Curie and Joliot reported that certain light elements (boron, magnesium, aluminum) which had been bombarded with alpha particles continued to emit positrons for some time after the bombardment was stopped. In other words, alpha-particle bombardment produced radioactive forms of boron, magnesium, and aluminum. Curie and Joliot actually measured half-lives of 14 minutes, 2.5 minutes, and 3.25 minutes, respectively for the radioactive substances formed by the alpha particle bombardment.
1.28. This result stimulated similar experiments all over the world. In particular, E. Fermi reasoned that neutrons, because of their lack of charge, should be effective in penetrating nuclei, especially those of high atomic number which repel protons and alpha particles strongly. He was able to verify his prediction almost immediately, finding that the nucleus of the bombarded atom captured the neutron and that there was thus produced an unstable nucleus which then achieved stability by emitting an electron. Thus, the final, stable nucleus was one unit higher in mass number and one unit higher in atomic number than the initial target nucleus.
1.29. As a result of innumerable experiments carried out since 1934, radioactive isotopes of nearly every element in the periodic table can now be produced. Some of them revert to stability by the emission of positrons, some by the emission of electrons, some by a process known as K-electron capture which we shall not discuss, and a small number (probably three) by alpha particle emission. Altogether some five hundred unstable nuclear species have been observed, and in most cases their atomic numbers and mass numbers have been identified.
1.30. Not only do these artificially radioactive elements play an important role throughout the project with which we are concerned, but their future value in medicine, in "tracer" chemistry, and in many other fields of research can hardly be overestimated.
ENERGY CONSIDERATIONS
NUCLEAR BINDING ENERGIES
1.31. In describing radioactivity and atomic structure we have deliberately avoided quantitative data and have not mentioned any applications of the equivalence of mass and energy which we announced as the guiding principle of this report. Now we must speak of quantitative details, not merely of general principles.
1.32. We have spoken of stable and unstable nuclei made up of assemblages of protons and neutrons held together by nuclear forces. It is a general principle of physics that work must be done on a stable system to break it up. Thus, if an assemblage of neutrons and protons is stable, energy must be supplied to separate its constituent particles. If energy and mass are really equivalent. then the total mass of a stable nucleus should be less than the total mass of the separate protons and neutrons that go to make it up. This mass difference, then, should be equivalent to the energy required to disrupt the nucleus completely, which is called the binding energy. Remember that the masses of all nuclei were "approximately" whole numbers. It is the small differences from whole numbers that are significant.
1.33. Consider the alpha particle as an example. It is stable; since its mass number is four and its atomic number two it consists of two protons and two neutrons. The mass of a proton is 1.00758 and that of a neutron is 1.00893 (see Appendix 2), so that the total mass of the separate components of the helium nucleus is
2 x 1.00758 + 2 x 1.00893 = 4.03302
whereas the mass of the helium nucleus itself is 4.00280. Neglecting the last two decimal places we have 4.033 and 4.003, a difference of 0.030 mass units. This, then, represents the "binding energy" of the protons and neutrons in the helium nucleus. It looks small, but recalling Einstein's equation, E = mc2, we remember that a small amount of mass is equivalent to a large amount of energy. Actually 0.030 mass units is equal to 4.5 × 10-6 ergs per nucleus or 2.7 × 1019 ergs per gram molecule of helium. In units more familiar to the engineer or chemist, this means that to break up the nuclei of all the helium atoms in a gram of helium would require 1.62 × 1011 gram calories or 190,000 kilowatt hours of energy. Conversely, if free protons and neutrons could be assembled into helium nuclei, this energy would be released.
1.34. Evidently it is worth exploring the possibility of getting energy by combining protons and neutrons or by transmuting one kind of nucleus into another. Let us begin by reviewing present-day knowledge of the binding energies of various nuclei.