Atomic Energy for Military Purposes (The Smyth Report)
The Official Report on the Development of the Atomic Bomb Under the Auspices of the United States Government
APPENDIX 4. THE FIRST SELF-SUSTAINING CHAIN REACTION PILE
In Chapter VI the construction and operation of the first self sustaining chain-reacting pile were described briefly. Though details must still be withheld for security reasons, the following paragraphs give a somewhat fuller description based on a report by Fermi. This pile was erected by Fermi and his collaborators in the fall of 1942.
DESCRIPTION OF THE PILE
The original plan called for an approximately spherical pile with the best materials near the center. Actually control measurements showed that the critical size had been reached before the sphere was complete, and the construction was modified accordingly. The final structure may be roughly described as an oblate spheroid flattened at the top, i.e., like a door knob. It was desired to have the uranium or uranium oxide lumps spaced in a cubic lattice imbedded in graphite. Consequently, the graphite was cut in bricks and built up in layers, alternate ones of which contained lumps of uranium at the corners of squares. The critical size was reached when the pile had been built to a height only three quarters of that needed according to the most cautious estimates. Consequently only one more layer was added. The graphite used was chiefly from the National Carbon Company and the Speer Carbon Company. The pile contained 12,400 lbs. of metal, part of which was supplied by Westinghouse, part by Metal Hydrides, and part by Ames. Since there were many more lattice points than lumps of metal, the remaining ones were filled with pressed oxide lumps.
For purposes of control and experiment there were ten slots passing completely through the pile. Three of those near the center were used for control and safety rods. Further to facilitate experiment, particularly the removal of samples, one row of graphite bricks carrying uranium and passing near the center of the pile was arranged so that it could be pushed completely out of the pile.
This whole graphite sphere was supported by a timber framework resting on the floor of a squash court under the West Stands of Stagg Field.
PREDICTED PERFORMANCE OF THE PILE
The metal lattice at the center of the pile and the two other major lattices making up the bulk of the rest of the pile had each been studied separately in exponential experiments #18, #27, and #29. These had given a multiplication factor of 1.07 for the metal lattice and 1.04 and 1.03 for the oxide lattices, the difference in the last two resulting from difference in the grade of graphite used. It is to be remembered that these figures are multiplication factors for lattices of infinite size. Therefore a prediction of the actual effective multiplication factor keff for the pile as constructed depended on the validity of the deduction of k from the exponential experiments, on a proper averaging for the different lattices, and on a proper deduction of keff from the average k for infinite size. Although the original design of the pile had been deliberately generous, its success when only partly completed indicated that the values of the multiplication factors as calculated from exponential experiments had been too low. The observed effective multiplication factor of the part of the planned structure actually built was about 1.0006 when all neutron absorbers were removed.
MEASUREMENTS PERFORMED DURING CONSTRUCTION
A series of measurements was made while the pile was being assembled in order to be sure that the critical dimensions were not reached inadvertently. These measurements served also to check the neutron multiplication properties of the structure during assembly, making possible a prediction of where the critical point would be reached.
In general, any detector of neutrons or gamma radiation can be used for measuring the intensity of the reaction. Neutron detectors are somewhat preferable since they give response more quickly and are not affected by fission-product radiations after shut down. Actually both neutron detectors (boron trifluoride counters) and gamma-ray ionization chambers were distributed in and around the pile. Certain of the ionization chambers were used to operate recording instruments and automatic safety controls.
In the pile itself measurements were made with two types of detector. A boron trifluoride counter was inserted in a slot about 43" from the ground and its readings taken at frequent intervals. In addition, an indium foil was irradiated every night in a position as close as possible to the effective center of the pile, and its induced activity was measured the following morning and compared with the readings of the boron trifluoride counter.
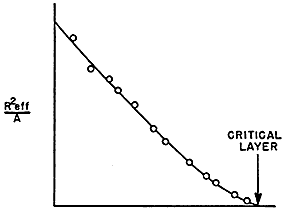
The results of such measurements can be expressed in two ways. Since the number of secondary neutrons produced by fission will increase steadily as the pile is constructed, the activity A induced in a standard indium foil at the center will increase steadily as the number of layers of the pile is increased. Once the effective multiplication factor is above one, A would theoretically increase to infinity. Such an approach to infinity is hard to observe, so a second way of expressing the results was used. Suppose the lattice spacing and purity of materials of a graphite-uranium structure are such that the multiplication factor would be exactly one if the structure were a sphere of infinite radius. Then, for an actual sphere of similar construction but finite radius, the activation of a detector placed at the center would be proportional to the square of the radius. It was possible to determine a corresponding effective radius Reff for the real pile in each of its various stages. It followed, therefore, that, if the factor k_infinity were precisely one on the average for the lattice in the pile, the activity A of the detector at the center should increase with increasing Reff in such a way that (Reff)2/A remained constant, but, if k_infinity for the lattice were greater than one, then as the pile size approached the critical value, that is, as k_infinity approached one, A should approach infinity and therefore (Reff)2/A approach zero. Therefore by extrapolating a curve of (Reff)2/A vs. size of the pile i.e., number of layers to where it cut the axis, it was possible to predict at what layer keff would become one. Such a curve [not shown here, but it's just a linear graph with negative gradient. Y-axis is (Reff)2/A and X-axis is the number of completed layers. Critical layer is the X-axis intercept.] indicated at what layer the critical size would be reached. The less useful but more direct and dramatic way of recording the results is,
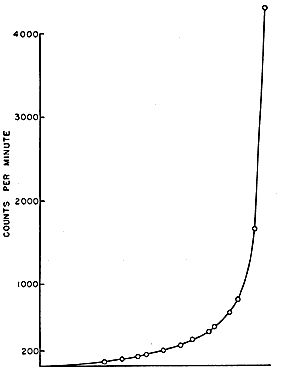
which shows the growth of the neutron activity of the pile as layers were added.
During the construction, appreciably before reaching this critical layer, some cadmium strips were inserted in suitable slots. They were removed once every day with the proper precautions in order to check the approach to the critical conditions. The construction was carried in this way to the critical layer.
CONTROL
The reaction was controlled by inserting in the pile some strips of neutron-absorbing material - cadmium or boron steel. When the pile was not in operation, several such cadmium strips were inserted in a number of slots, bringing the effective multiplication factor considerably below one. In fact, any one of the cadmium strips alone was sufficient to bring the pile below the critical condition. Besides cadmium strips that could be used for manual operation of the pile, two safety rods and one automatic control rod were provided. The automatic control rod was operated by two electric motors responding to an ionization chamber and amplifying system so that, if the intensity of the reaction increased above the desired level, the rod was pushed in, and vice versa.
OPERATION OF THE PILE
To operate the pile all but one of the cadmium strips were taken out. The remaining one was then slowly pulled out. As the critical conditions were approached, the intensity of the neutrons emitted by the pile began to increase rapidly. It should be noticed, however, that, when this last strip of cadmium was so far inside the pile that the effective multiplication factor was just below one, it took a rather long time for the intensity to reach the saturation value. Similarly, if the cadmium strip was just far enough out to make keff greater than one, the intensity rose at a rather slow rate. For example, if one rod is only 1 cm. out from the critical position, the "relaxation time," i.e., the time for the intensity to double, is about four hours. These long "relaxation times" were the result of the small percentage of delayed neutrons which have been discussed in Appendix 3, and make it relatively easy to keep the pile operating at a constant level of intensity.
The pile was first operated on December 2, 1942 to a maximum energy production of about ½ watt. On December 12th the intensity was run up to about 200 watts, but it was not felt safe to go higher because of the danger of the radiation to personnel in and around the building. During this high intensity run, measurements were made of radiation intensity beside the pile, in the building, and on the sidewalk outside.